A block of mass 2 kg is pushed against a rough vertical wall with a force is 40 N. Coefficient of static friction being 0.5. Another horizontal force is 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
To determine whether the block will move and in which direction, we will analyze the forces acting on the block step by step.
Step 1: Identify the forces acting on the block
- Weight (W): The weight of the block is given by W=mg=2kg×10m/s2=20N acting downwards.
- Applied Force (F1): A force of 40N is pushing the block against the wall.
- Horizontal Force (F2): A horizontal force of 15N is applied parallel to the wall.
- Normal Force (N): The wall exerts a normal force on the block, which acts perpendicular to the wall.
- Frictional Force (f): The frictional force opposes the motion of the block.
Step 2: Calculate the normal force (N)
Since the block is pushed against the wall with a force of 40N, the normal force N exerted by the wall on the block is equal to this applied force:
N=F1=40N
Step 3: Calculate the maximum static friction force (f_max)
The maximum static friction force can be calculated using the formula:
fmax=μs⋅N
Where μs=0.5 (coefficient of static friction).
fmax=0.5×40N=20N
Step 4: Determine the net force acting on the block
The block experiences a horizontal force F2=15N acting to the right. The frictional force will act to the left to resist this motion. The net force Fnet can be calculated as:
Fnet=F2−f
Where f is the frictional force. Since we need to check if the block will move, we will first assume that it does not move, so:
f=fmax=20N
Now substituting:
Fnet=15N−20N=−5N
Step 5: Analyze the result
Since Fnet<0, this indicates that the frictional force is sufficient to prevent the block from moving. Therefore, the block will not move.
Step 6: Find the actual frictional force (f)
Since the block does not move, the frictional force will equal the horizontal force applied, but in the opposite direction:
f=F2=15N
Conclusion
The block will not move, and the frictional force exerted by the wall on the block is 15N acting to the left.
---
- Weight (W): The weight of the block is given by W=mg=2kg×10m/s2=20N acting downwards.
- Applied Force (F1): A force of 40N is pushing the block against the wall.
- Horizontal Force (F2): A horizontal force of 15N is applied parallel to the wall.
- Normal Force (N): The wall exerts a normal force on the block, which acts perpendicular to the wall.
- Frictional Force (f): The frictional force opposes the motion of the block.
Since the block is pushed against the wall with a force of 40N, the normal force N exerted by the wall on the block is equal to this applied force:
N=F1=40N
The maximum static friction force can be calculated using the formula:
fmax=μs⋅N
Where μs=0.5 (coefficient of static friction).
fmax=0.5×40N=20N
The block experiences a horizontal force F2=15N acting to the right. The frictional force will act to the left to resist this motion. The net force Fnet can be calculated as:
Fnet=F2−f
Where f is the frictional force. Since we need to check if the block will move, we will first assume that it does not move, so:
f=fmax=20N
Fnet=15N−20N=−5N
Since Fnet<0, this indicates that the frictional force is sufficient to prevent the block from moving. Therefore, the block will not move.
Since the block does not move, the frictional force will equal the horizontal force applied, but in the opposite direction:
f=F2=15N
The block will not move, and the frictional force exerted by the wall on the block is 15N acting to the left.
Topper's Solved these Questions
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Questions for short Answer
Explore 11 Videos
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Objective -2
Explore 5 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
- GRAVITATIONBook:HC VERMA ENGLISHChapter:GRAVITATIONExercise:Question for short Answers
Explore 18 Videos
Similar Questions
A block of mass 2 kg is pushed against a rough vertical wall with a force of 40N. Coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionA block of mass 1kg is pushed against a rough vertical wall with a force of 20N, coefficient of static friction being 14 Another horizontal force of 10N is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction ? If no, find the frictional force exerted by the wall on the block. (g=10m/s2)
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
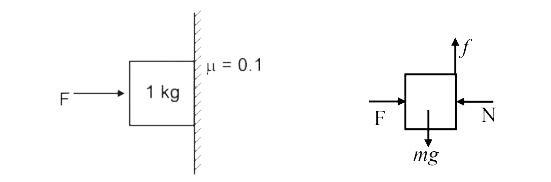
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionA block of mass 2 kg is pressed against a rigid vertical wall by a horizontal force of 100 N. If co-efficient of static and kinetic friction are each equal to 0.3 then find the magnitude and direction of frictional force on the block.

View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution