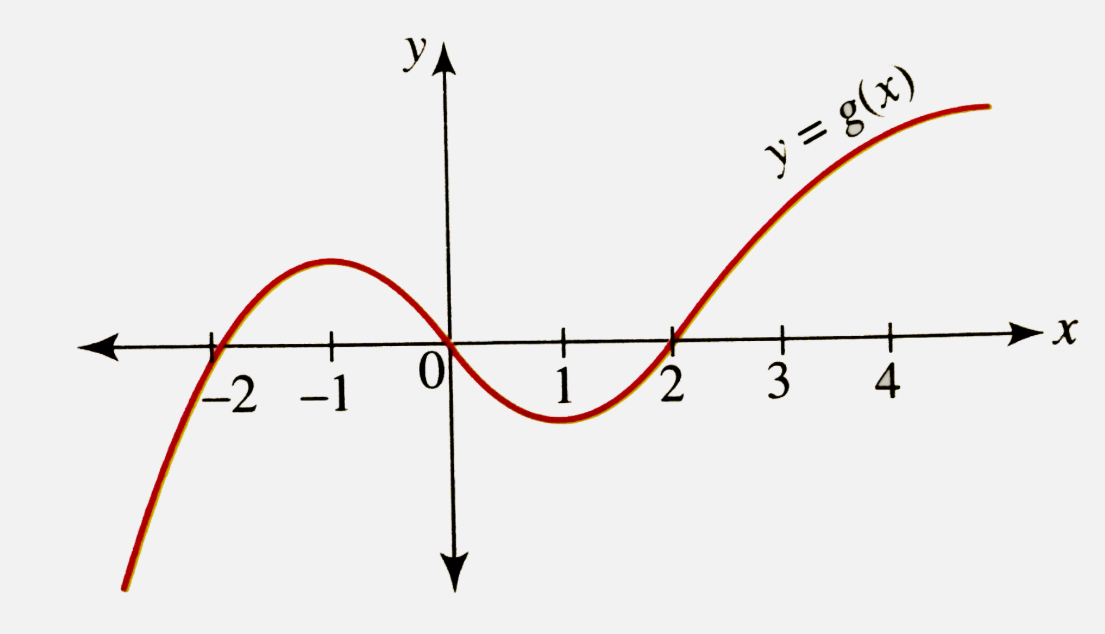
For the function g whose graph is given. Arrange the following numbers in increasing order and explain your reasoning.
$g (0), g' (- 2), g' (0), g' (2), g' (4)$

Video Solution

Text Solution

Verified by Experts

From the graph, the value of f(0) = 0.
Also tangent to $y = g (x) at x = 0$ makes an obtuse angle with the positive x - axis, hence $g' (0) < 0$ .
The measure of acute angle of inclination with the positive x - axis for tangent at $x = - 2, x = 2, x = 4$ is in decreasing order.
Hence $g' (- 2), > g' (2) > g' (4)$ .
Thus, values in increasing order are $g' (0) < g (0) < g' (4) < g' (2) < g' (- 2)$ .

Updated on:21/07/2023

If $G^{2} < G$ , which of the following could be G ?
A1
B $\frac{23}{7}$
C $\f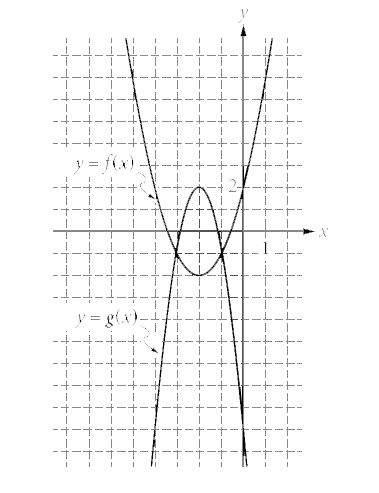rac{7}{23}$
D $- 4$
Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does $f (x) + g (x) = 0$ ?
A $- 3$
B $- 2$
C $- 1$
D0
In the xy-plane, the graph of the functions g has zeros at -4, 2, and 4. Which of the following could define g?
A $g (x) = (x - 4) (x - 2) (x + 4)$
B $g (x) = {(x - 4)}^{2} (x - 2)$
C $g (x) = (x - 4) (x + 2) (x + 4)$
D $g (x) = (x + 2) {(x + 4)}^{2}$