In the xy-plane, the graph of the functions g has zeros at -4, 2, and 4. Which of the following could define g?
The correct Answer is:A
To solve the problem, we need to find a function g(x) that has zeros at x=−4, x=2, and x=4. This means that when we substitute these values into the function g(x), the output should be zero.
1. Understanding Zeros of a Function:
- A function g(x) has a zero at x=a if g(a)=0. Given that g has zeros at −4, 2, and 4, we can express this mathematically.
2. Formulating the Function:
- The zeros of the function indicate that g(x) can be expressed as a product of factors corresponding to these zeros. Specifically, if g has zeros at x=−4, x=2, and x=4, we can write:
g(x)=k(x+4)(x−2)(x−4)
- Here, k is a constant that can be any non-zero value (often set to 1 for simplicity).
3. Writing the Function:
- For simplicity, let’s assume k=1. Thus, we can write:
g(x)=(x+4)(x−2)(x−4)
4. Expanding the Function:
- We can expand this function if needed, but for the purpose of identifying the function that defines g, it is sufficient to leave it in factored form.
5. Conclusion:
- Therefore, one possible definition of g that has zeros at the specified points is:
g(x)=(x+4)(x−2)(x−4)
- A function g(x) has a zero at x=a if g(a)=0. Given that g has zeros at −4, 2, and 4, we can express this mathematically.
- The zeros of the function indicate that g(x) can be expressed as a product of factors corresponding to these zeros. Specifically, if g has zeros at x=−4, x=2, and x=4, we can write:
g(x)=k(x+4)(x−2)(x−4)
- Here, k is a constant that can be any non-zero value (often set to 1 for simplicity).
- For simplicity, let’s assume k=1. Thus, we can write:
g(x)=(x+4)(x−2)(x−4)
- We can expand this function if needed, but for the purpose of identifying the function that defines g, it is sufficient to leave it in factored form.
- Therefore, one possible definition of g that has zeros at the specified points is:
g(x)=(x+4)(x−2)(x−4)
Topper's Solved these Questions
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 15: GRID-INS
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 16: MORE GRID-INS
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 13: ADVANCED GEOMETRY
Explore 11 Videos
- PRACTICE TEST 4Book:PRINCETONChapter:PRACTICE TEST 4Exercise:Math Test-Calculator
Explore 38 Videos
- SAT MATH: THE BIG PICTUREBook:PRINCETONChapter:SAT MATH: THE BIG PICTUREExercise:Example
Explore 4 Videos
Similar Questions
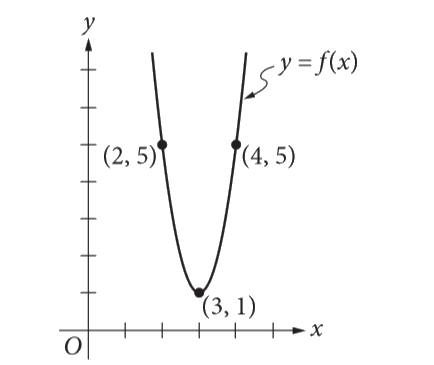
The graph of the function f in the xy-plane above is a parabola. Which of the following defines f ?
View SolutionThe graph of the exponential function h in the xy-plane, where y = h(x), has a y-intercept of d, where d is a positive constant. Which of the following could define the function h ?
View Solution
Knowledge Check
In the xy-plane, the graph of function f has x-intercepts at -3, -1, and 1. Which of the following could define f ?
Af(x)=(x−3)(x−1)(x+1)Bf(x)=(x−3)(x−1)2Cf(x)=(x−1)(x+1)(x+3)Df(x)=(x+1)2(x+3)If G2<G, which of the following could be G ?
A1B237C723D−4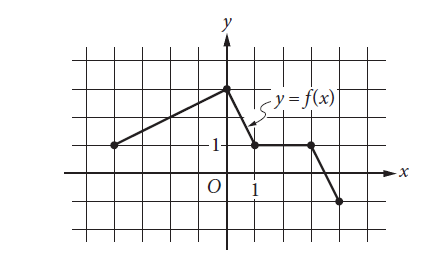
The complete graph of the function f is shown in the xy-plane above. Which of the following are equal to 1 ?
I. f(−4)
II. f(32)
III. f(3)AIII onlyBI and III onlyCII and III onlyDI, II, and III
In the xy -plane, the graph of the function f(x)=x2+5x+4 has two x -intercepts. What is the distance between the x-intercepts?
View SolutionIn the xy-plane, the graph of which of the following equations is a line with a slope of 3 ?
View SolutionThe zeros of the polynomial function g are 4 and -2. If the range of g is the set real numbers greater than or equal to -3, which of the following could be the graph of y=g(x) in the xy-plane?
View SolutionIF f(x)=√x and the composite function f(g(x))=√4x2−5, which of the following could be g(x) ?
View SolutionIf the function f has three distinct zeros, which of the following represents the graph of f in the xy-plane?
View Solution

