The diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
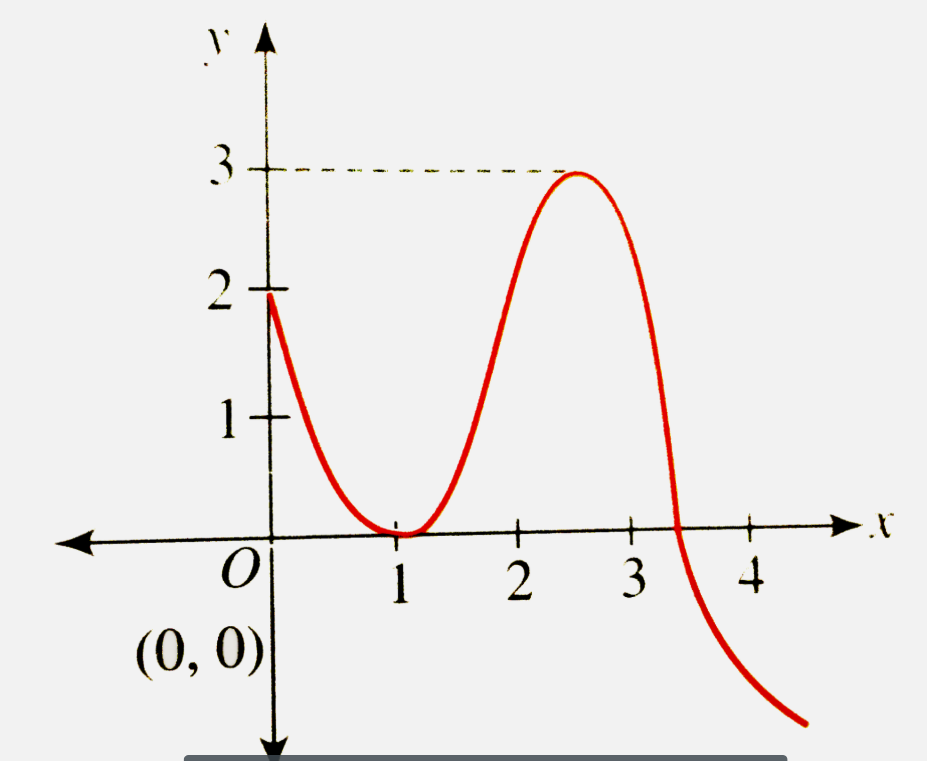
(a) Tangent line to y = f(x) at x = 0 makes an angle of sec−1√5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
Slope of y tangent at x=0istan−1(2)=sec−1√5.
Hence (a) is correct.
f'(x)≥0 for x∈(0,3), hence f is increasing for (0, 3) , and so (b) is correct.
The x - axis is tangent to the curve at x = 1, therefore f''(1) = 0.
So x = 1 is point of inflection, but not the point of extremum as the sign of f'(x) does not change at x = 1.
Hence (c) is not correct.
Obviously, y = f(x) has two critical points as f'(1) = 0 and f'(3.5) = 0.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.22
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.23
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.20
1 Videos
- FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
If f''(x)∣≤1∀x∈R,andf(0)=0=f'(0), then which of the following can not be true ?
View SolutionFollowing is the graph of y = f(x).
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_GRA_C01_S01_005_Q01.pngwh=80%mx-autosty≤=background:white;><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.
View Solution
Knowledge Check
If f(x)=[4x]−2x with domain 0≤x≤2, then f(x) can also be written as
A2xB−xC−2xDnone of the above
If f''(x)≤0for allx∈(a,b) then f'(x)=0
View SolutionIf f''(x)=sec2x and f (0) = f '(0) = 0 then:
View SolutionDraw the graph of function f(x)={x 0≤x≤1[x] 1≤x≤2. Graphically comment on the monotonic behaviour of f(x) at x=1 . Is f(x) M.I. for X∈[0,2]
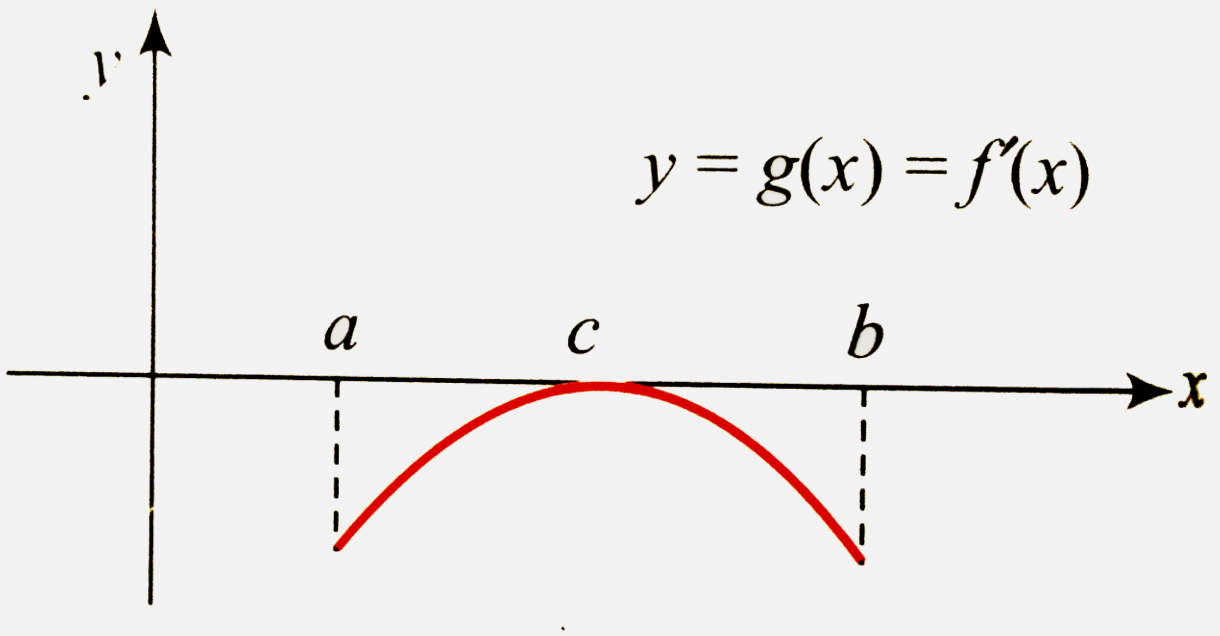
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionLet f(x)=x(2−x),0≤x≤2. If the definition of f(x) is extended over the set R−[0,2] by f(x+1)=f(x), then f is a
View SolutionIf f(x) and g(x) are differentiable function for 0≤x≤23 such that f(0) =2, g(0) =0 ,f(23) =22 g (23) =10. Then show that f'(x)=2g'(x) for at least one x in the interval (0,23)
View SolutionIf f(x+y)=f(x)+f(y)+|x|y+xy2,∀x,y∈Randf'(0)=0, then
View Solution
