In the following graph, state the absolute and local maximum and minimum values of the function.
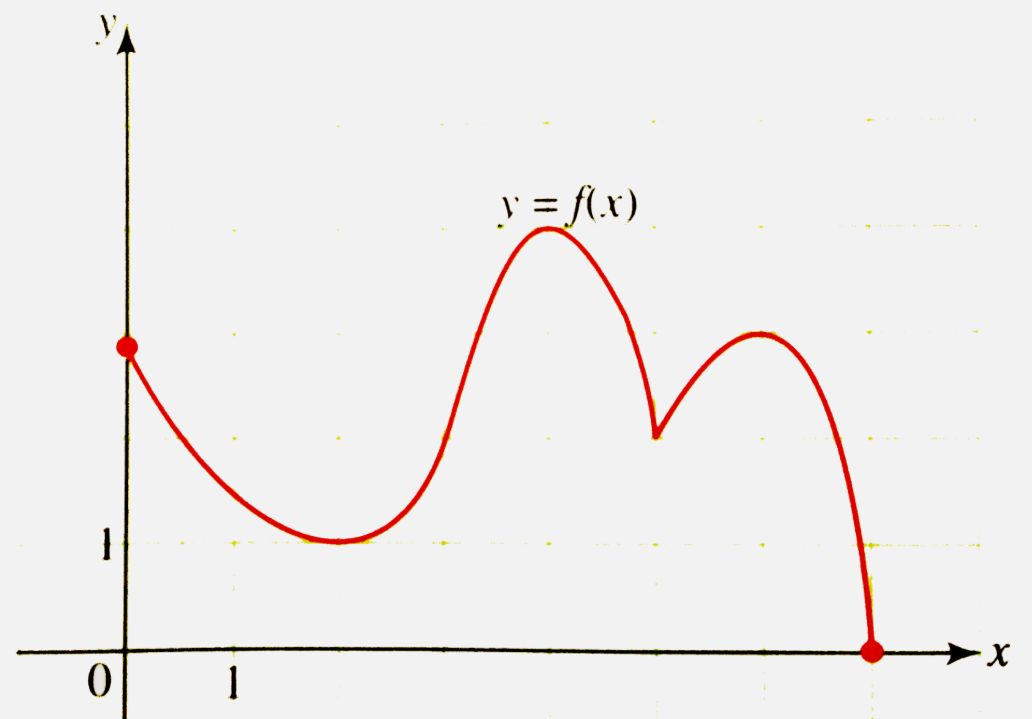
x = 2 is the point of local minima, and the local minimum value is f(2) = 1.
x = 4 is the point of absolute maxima, and the absolute maximum value is f(4) = 4.
x = 5 is the point of local minima, and the local minimum value is f(5) = 2.
x = 6 is the point of local maxima, and the local maximum value is f(6) = 3.
x = 7 is the point of absolute minima, and the local minimum value is f (7) = 0.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.23
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.24
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.21
1 Videos
- FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
Find the maximum and minimum values of the function f(x)=tanx−2x .
View SolutionFind local maximum and local minimum values of the function f given byf(x)=3x4+4x3−12x2+12.
View SolutionFind the maximum and minimum values of the following functions.
f(x)=sinx+√3cosx
View SolutionFind the maximum and minimum values of the following functions.
f(x)=x3−2x2+x+6
View SolutionFind all the points of local maxima and local minima as well as the corresponding local maximum and local minimum values for the function f(x)=(x−1)3(x+1)2 .
View SolutionFind the absolute maximum/minimum value of following function
f(x)=x3 for x∈[−2,2].
View SolutionFind the maximum or minimum values of the following functions:
(i)x3−2x2+x+3
View SolutionFind all the points of local maxima and minima and the corresponding maximum and minimum values of the function f(x)=−34x4−8x3−452x2+105 .
View SolutionFind all the points of local maxima and minima and the corresponding maximum and minimum values of the function f(x)=−34x4−8x3−452x2+105 .
View SolutionFind all the points of local maxima and minima and the corresponding maximum and minimum values of the function f(x)=2x3−21x2+36x−20 .
View Solution
