The graph of a function is shown in the following figure.
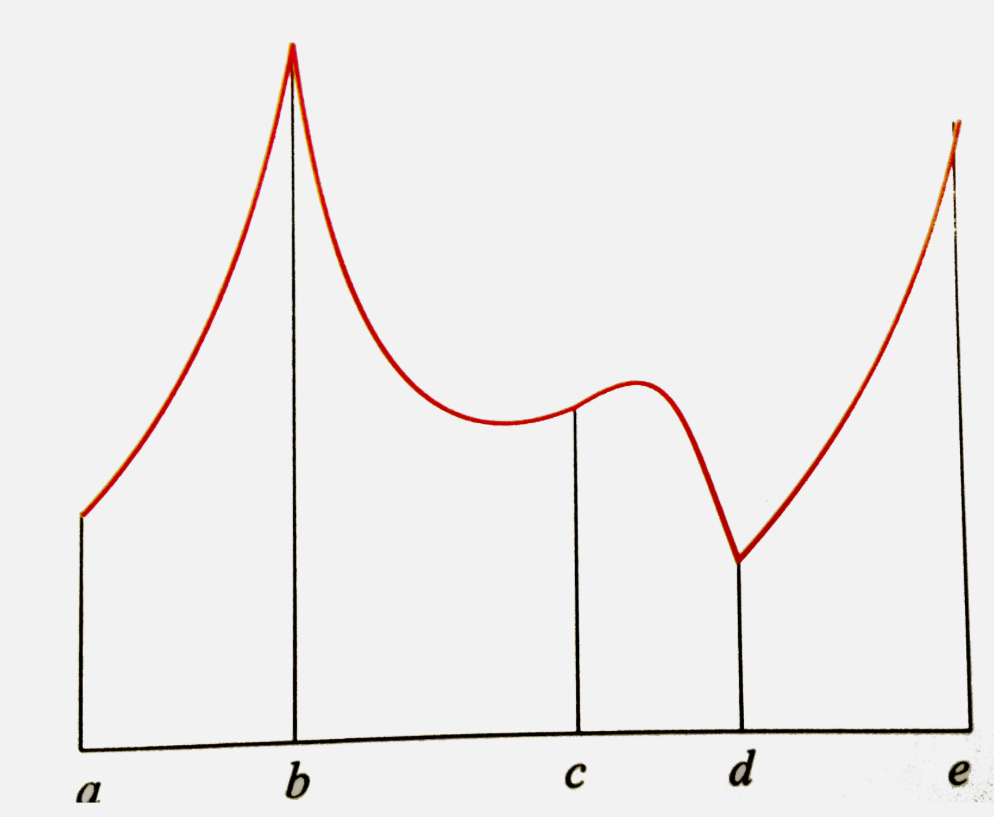
Determine the intervals on which the function is concave up and the intervals on which it is concave down. Find the x - coordinates of any inflection points.
The graph is concave up on a<x<b,b<x<candd<x<e. The graph is concave down on c<x<d.
Note that concavity is a property of a graph on an open interval, so the endpoints are not included.
There are inflection points at x = c and x = d.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBook:CENGAGE ENGLISHChapter:GETTING STARTED WITH GRAPHSExercise:ILLUSTRATION 1.20
Explore 1 Video
- GETTING STARTED WITH GRAPHSBook:CENGAGE ENGLISHChapter:GETTING STARTED WITH GRAPHSExercise:ILLUSTRATION 1.21
Explore 1 Video
- GETTING STARTED WITH GRAPHSBook:CENGAGE ENGLISHChapter:GETTING STARTED WITH GRAPHSExercise:ILLUSTRATION 1.18
Explore 1 Video
- FUNCTIONSBook:CENGAGE ENGLISHChapter:FUNCTIONSExercise:Comprehension Type
Explore 7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercises
Explore 18 Videos
Similar Questions
The graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.

View SolutionFind the interval in which the function f(x)=x2+2x,x<0 is decreasing.
View Solution
Knowledge Check
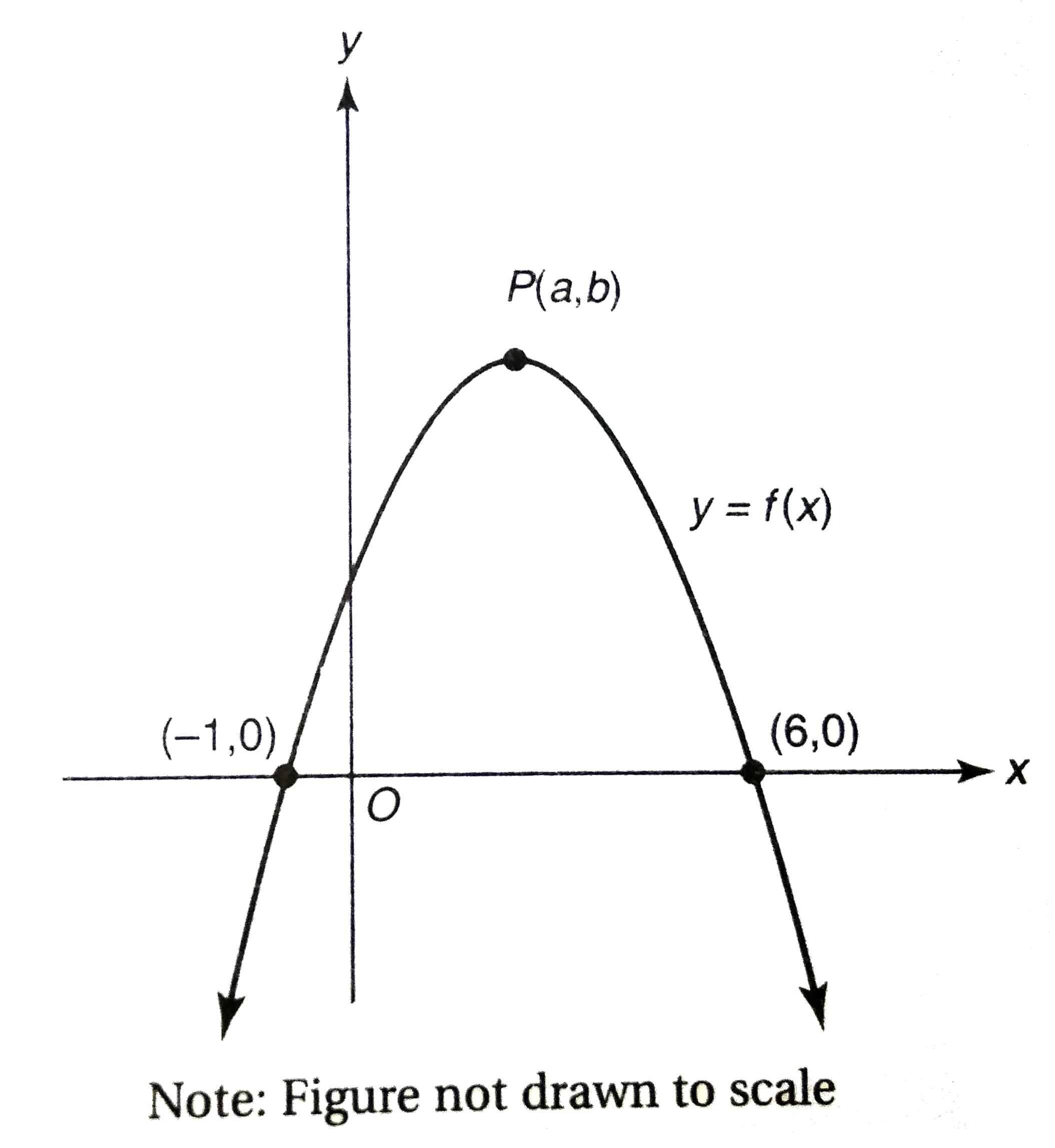
The graph of a quadratic function f is shown in the above figure. If f(x)≤b for all values of x, which of the following could be the coordinates of point P?A(1.5,2)B(2.25.3.5)C(2.5,4)D(2.75,5)Find the interval in which the function f(x)=√3sin2x−cos2x+4 is one - one
A[−π2,π2]B[−π6,π2]C[−π6,π3]D[−π6,π2]
The graph of the function f is shown above. Which of the following could represent the graph of y=|f(x)|?A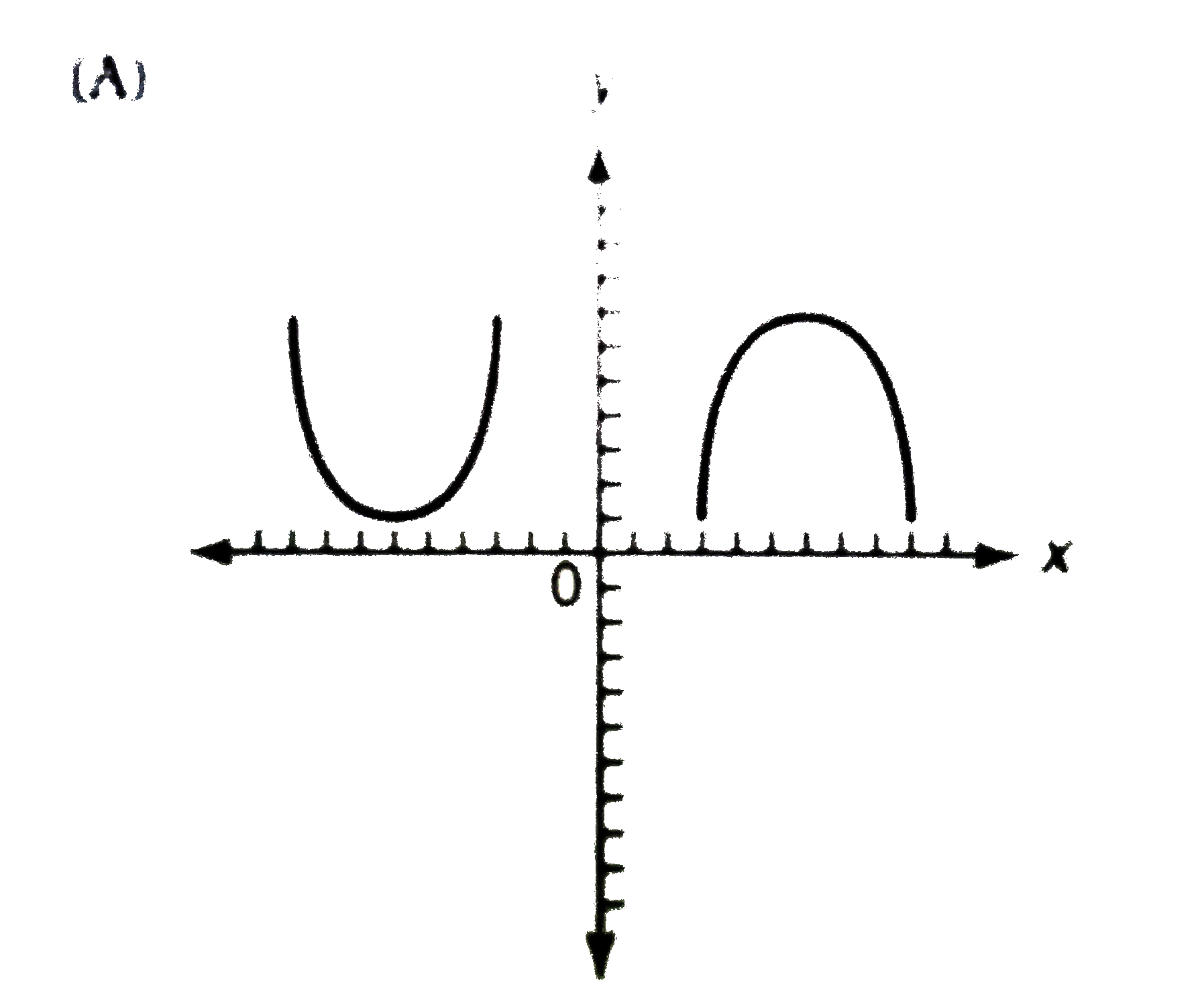 B
B C
C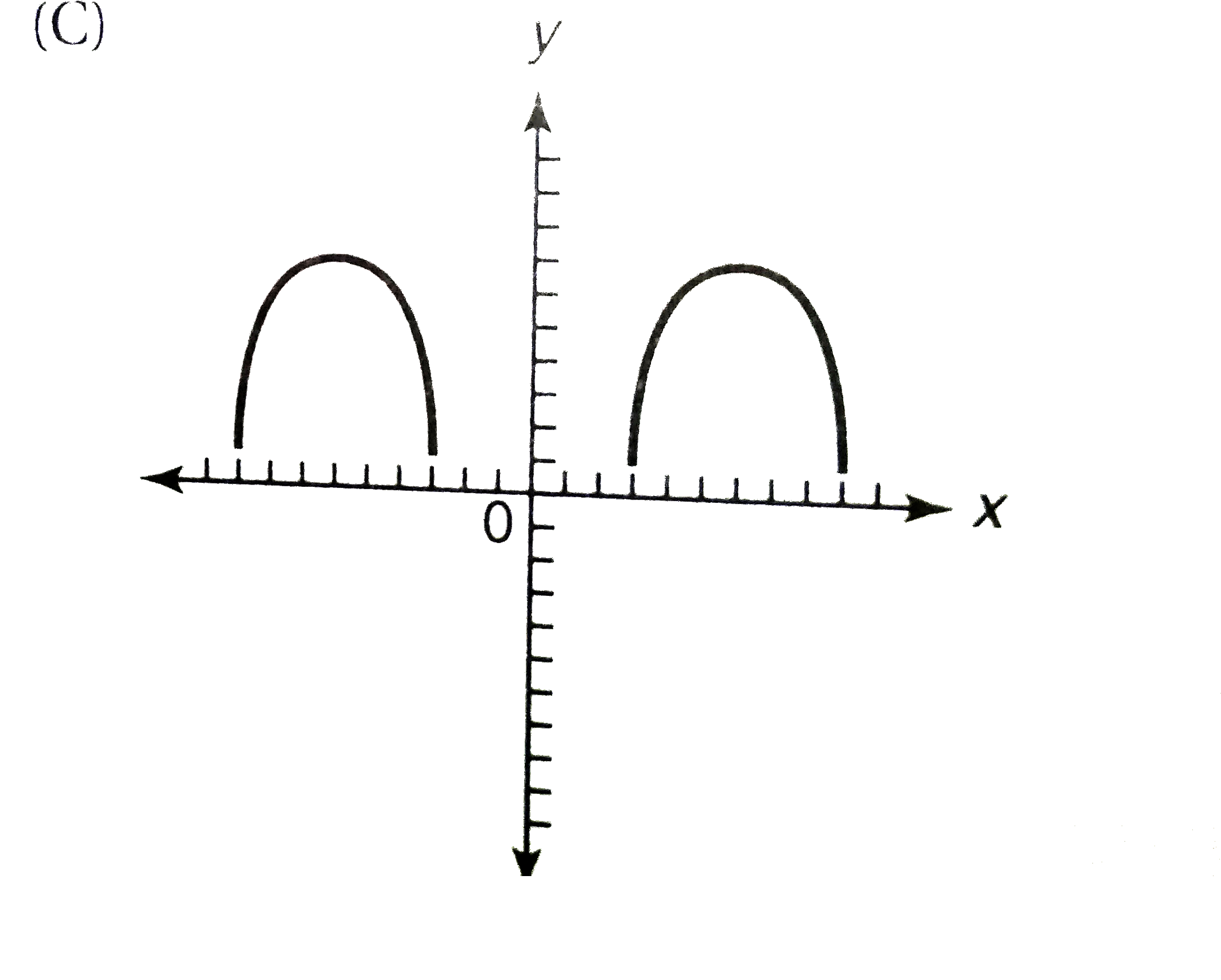 D
D
The graph of the function y=f(x) is shown in the adjacent figure then correct statement is

View SolutionFind the intervals in which the function f(x)=x4−x33 is increasing or decreasing.
View SolutionFind the intervals in which the function f(x)=x4−x33 is increasing or decreasing.
View SolutionThe interval in which the function f(x)=x2−4x+6 is strictly increasing is
View SolutionThe interval in which the function x3 increases less rapidly than 6x2+15x+5
View Solution