In which orientation,a diole placed, in a uniform field is in (i) stable (ii) unstable equilibrioum?
To determine the orientation of a dipole in a uniform electric field for stable and unstable equilibrium, we can analyze the potential energy of the dipole in relation to the electric field.
1. Understanding the Dipole in an Electric Field:
- A dipole consists of two equal and opposite charges separated by a distance. When placed in an electric field, it experiences a torque that tends to align it with the field.
2. Potential Energy of a Dipole:
- The potential energy (U) of a dipole in an electric field (E) is given by the formula:
U=−→p⋅→E=−pEcos(θ)
where →p is the dipole moment, E is the magnitude of the electric field, and θ is the angle between the dipole moment and the electric field.
3. Stable Equilibrium:
- A dipole is in stable equilibrium when it is in a position of minimum potential energy. This occurs when the angle θ is 0∘ (i.e., the dipole moment is parallel to the electric field).
- At this position, any small displacement will increase the potential energy, causing the dipole to return to this position.
- Thus, for stable equilibrium:
Orientation: θ=0∘ (parallel to the electric field)
4. Unstable Equilibrium:
- A dipole is in unstable equilibrium when it is in a position of maximum potential energy. This occurs when the angle θ is 180∘ (i.e., the dipole moment is anti-parallel to the electric field).
- At this position, any small displacement will decrease the potential energy, causing the dipole to move away from this position.
- Thus, for unstable equilibrium:
Orientation: θ=180∘ (anti-parallel to the electric field)
Final Answer:
- (i) Stable equilibrium: Dipole is parallel to the electric field (θ=0∘).
- (ii) Unstable equilibrium: Dipole is anti-parallel to the electric field (θ=180∘).
- A dipole consists of two equal and opposite charges separated by a distance. When placed in an electric field, it experiences a torque that tends to align it with the field.
- The potential energy (U) of a dipole in an electric field (E) is given by the formula:
U=−→p⋅→E=−pEcos(θ)
where →p is the dipole moment, E is the magnitude of the electric field, and θ is the angle between the dipole moment and the electric field.
- A dipole is in stable equilibrium when it is in a position of minimum potential energy. This occurs when the angle θ is 0∘ (i.e., the dipole moment is parallel to the electric field).
- At this position, any small displacement will increase the potential energy, causing the dipole to return to this position.
- Thus, for stable equilibrium:
Orientation: θ=0∘ (parallel to the electric field)
- A dipole is in unstable equilibrium when it is in a position of maximum potential energy. This occurs when the angle θ is 180∘ (i.e., the dipole moment is anti-parallel to the electric field).
- At this position, any small displacement will decrease the potential energy, causing the dipole to move away from this position.
- Thus, for unstable equilibrium:
Orientation: θ=180∘ (anti-parallel to the electric field)
- (i) Stable equilibrium: Dipole is parallel to the electric field (θ=0∘).
- (ii) Unstable equilibrium: Dipole is anti-parallel to the electric field (θ=180∘).
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set- II]
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set-III]
Explore 3 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-III, DELHI BOARD
Explore 4 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
If there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

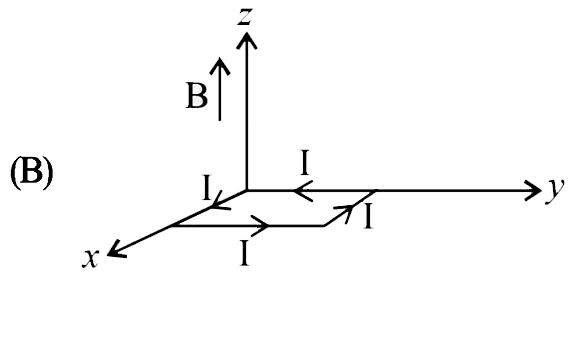

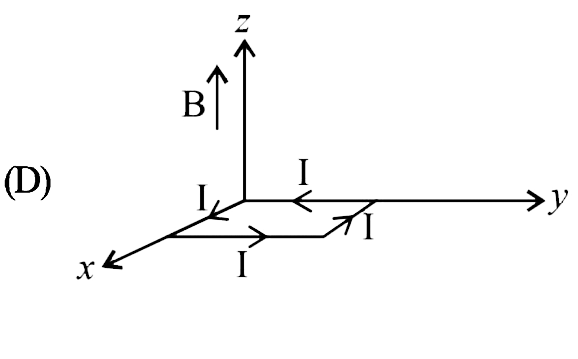
View SolutionA short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View Solution
Knowledge Check
A rectangular loop of sides 10cm and 5cm carrying a current I of 12A is placed in different orienctations as shown in the figure
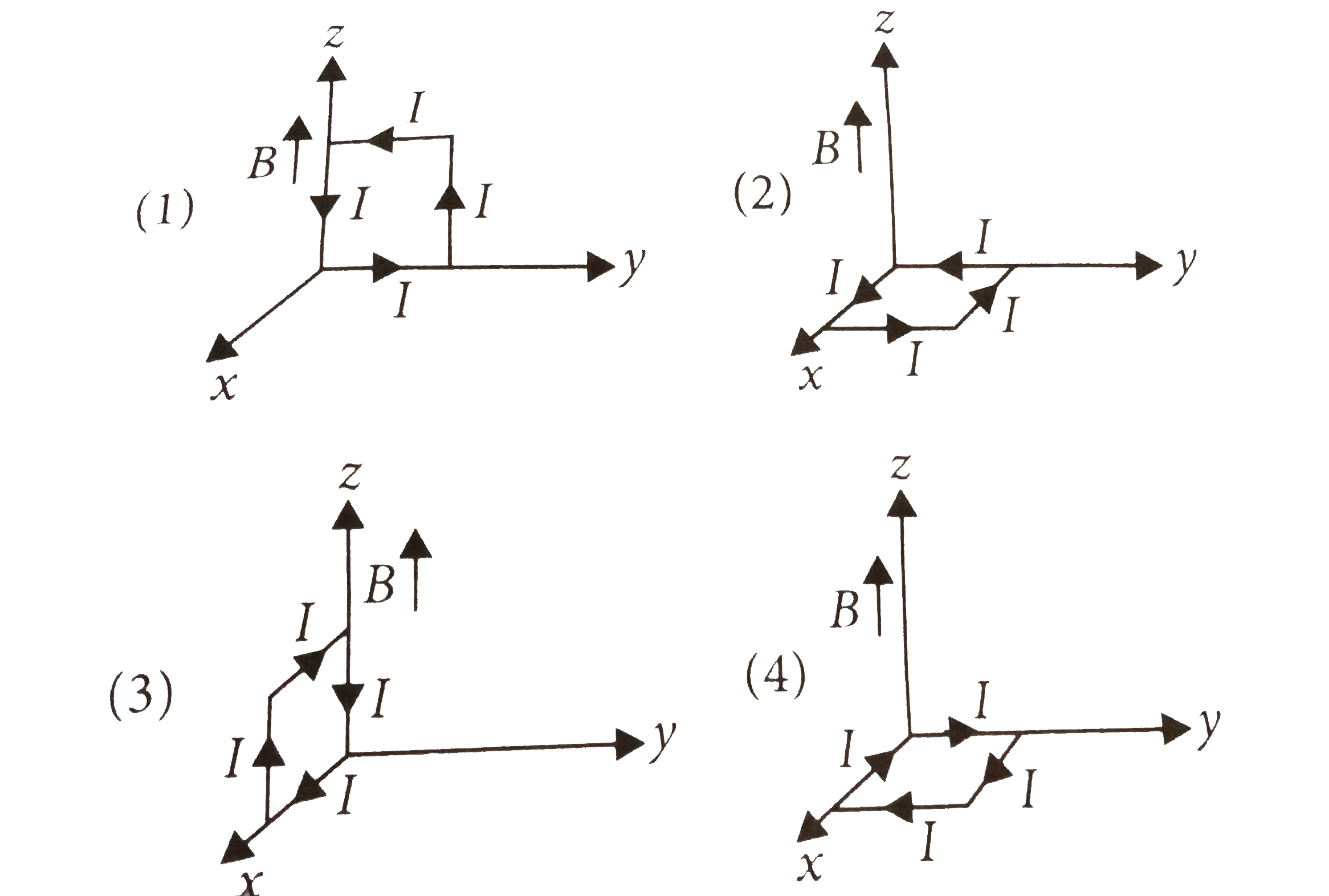
If there is a uniform magnetic field of 0.3 T in the positive z-direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium .A(2)and(4), respectivelyB(2)and(3), respectivelyC(1)and(2), respectivelyD(1)and(3), respectively
A short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View Solution(i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.
(ii) Depiet the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
View SolutionWhich orientation of an electric dipole in a uniform electric field would correspond to stable equilibrium ?
View SolutionAnswer the following:
(a) Derive an expression for the potential energy of an electric dipole in a uniform electric field. Explain conditions for stable and unstable equilibrium.
(b) Is the electrostatic potential necessarily zero at a point where the electric field is zero ? Give an example to support your answer.
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionAn electric dipole of dipole moment p is placed in a uniform electric field E in stable equilibrium position. Its moment of inertia about the centroidal axis is I . If it is displaced slightly from its mean position, find the period of small oscillations.
View SolutionA short bar magnet of magnetic moment 0⋅4JT−1 is placed in a uniform magnetic field of 0⋅16T. The magnet is in stable equilibrium when the potencial energy is
View Solution
