Question

Answer the following:

(a) Derive an expression for the potential energy of an electric dipole in a uniform electric field. Explain conditions for stable and unstable equilibrium.
(b) Is the electrostatic potential necessarily zero at a point where the electric field is zero ? Give an example to support your answer.

Explanation

(a) Let an electric, dipole of dipole moment `vecP` be placed in an electric field `vecE` making an angle `theta` with the direction of electric field intensity `vecE`.
The torque acting on the dipole is given by :
`vectau=vecPxxvecE`
`tau=PE sin theta`
work done to rotate the dipole through an angle `dtheta`
`d omega=tau d theta= PE sin theta d theta`
work done to rotate the dipole from `theta_(1)" to "theta_(2)`
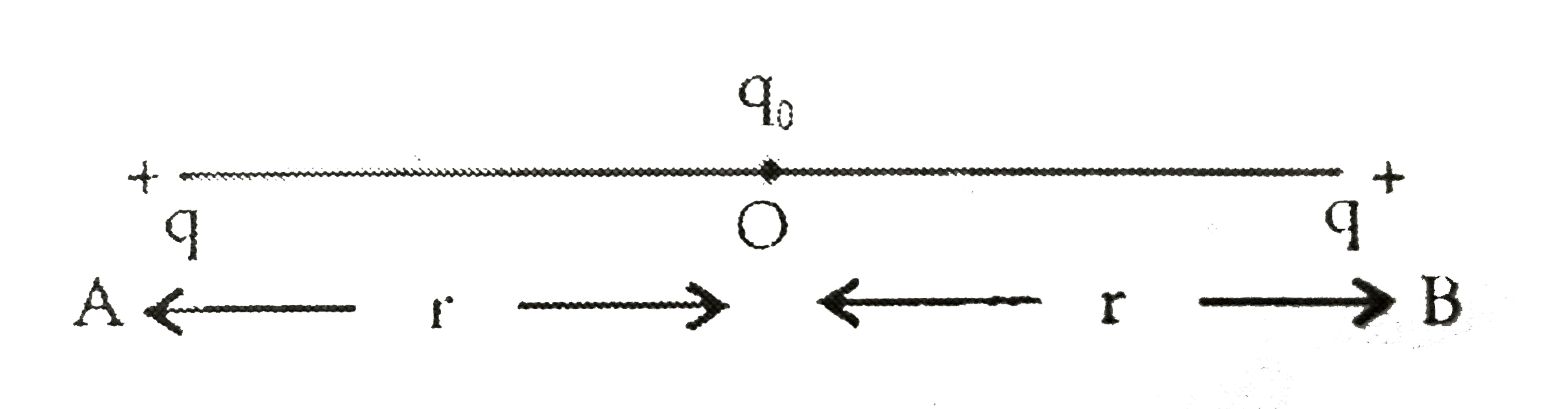
W=int_(theta_(1))^(theta_(2))PE sin theta d theta=PE[-cos theta]_(theta_(1))^(theta_(2))=-PE(cos theta_(2)-cos theta_(1))`
`"If "theta_(1)=90^(@) and theta_(2)=theta" "U=-PE cos theta =vecP.vecE`
for stable equilibrium `theta=0^(@) rArr tau = 0 rArr U=-PE`
for unstable equilibrium `theta=180^(@)rArr tau =0 rArr U = + PE.`
(b) No.
For Example : Let we have two positive charges of same magnitude are placed at point A and B respectively. Electric field at mid pint O is zero but the electrostatic potential is
`V=(1)/(4pi in_(0))(q)/(r)xx2`
`V=(1)/(4pi in_(0))(2q)/(r).`