In an electric dipole, at which point is the electric potential zero?
To determine the point at which the electric potential is zero in an electric dipole, we can follow these steps:
1. Understand the Electric Dipole: An electric dipole consists of two equal and opposite charges, +Q and -Q, separated by a small distance, denoted as '2L'.
2. Define the Electric Potential: The electric potential (V) due to a point charge is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
3. Identify the Point of Interest: Let's consider a point P located on the perpendicular bisector of the dipole. The distance from point P to the positive charge (+Q) is r1 and to the negative charge (-Q) is r2.
4. Calculate the Electric Potential at Point P:
- The potential at point P due to the positive charge (+Q):
V1=kQr1
- The potential at point P due to the negative charge (-Q):
V2=−kQr2
5. Express Distances: For point P, the distances can be expressed using the Pythagorean theorem. If the distance from the center of the dipole to point P is R, then:
r1=√L2+R2andr2=√L2+R2
6. Combine the Potentials: The total electric potential at point P is the sum of the potentials due to both charges:
V=V1+V2=kQr1−kQr2
7. Set the Total Potential to Zero: For the total potential to be zero:
V=kQr1−kQr2=0
This implies:
kQr1=kQr2
8. Conclusion: The electric potential is zero at points along the perpendicular bisector of the dipole, specifically at the equatorial line (the line that bisects the dipole at right angles).
Final Answer:
The electric potential is zero at points along the equatorial line of the electric dipole.
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
- The potential at point P due to the positive charge (+Q):
V1=kQr1
- The potential at point P due to the negative charge (-Q):
V2=−kQr2
r1=√L2+R2andr2=√L2+R2
V=V1+V2=kQr1−kQr2
V=kQr1−kQr2=0
This implies:
kQr1=kQr2
The electric potential is zero at points along the equatorial line of the electric dipole.
Similar Questions
(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
View SolutionAt what angle of electric dipole moment with uniform electric field, potential energy is maximum ?
View SolutionAn α particle is placed in an electric field at a point having electric potential 5V. Find its potential energy ?
View SolutionIn th electric potential on the axis of an electric dipole at a distance 'r' from it is V, then the potential at a point on its equatorial line at the same distance away frornt it will be
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
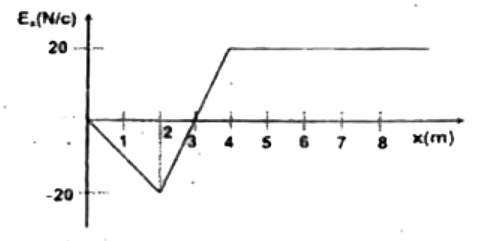
View SolutionTwo point charge - 5μC and + 3μC are placed 64 cm apart. At what points on the line joining the two charges is the electric potential zero. Assume the potential at infinity to be zero.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
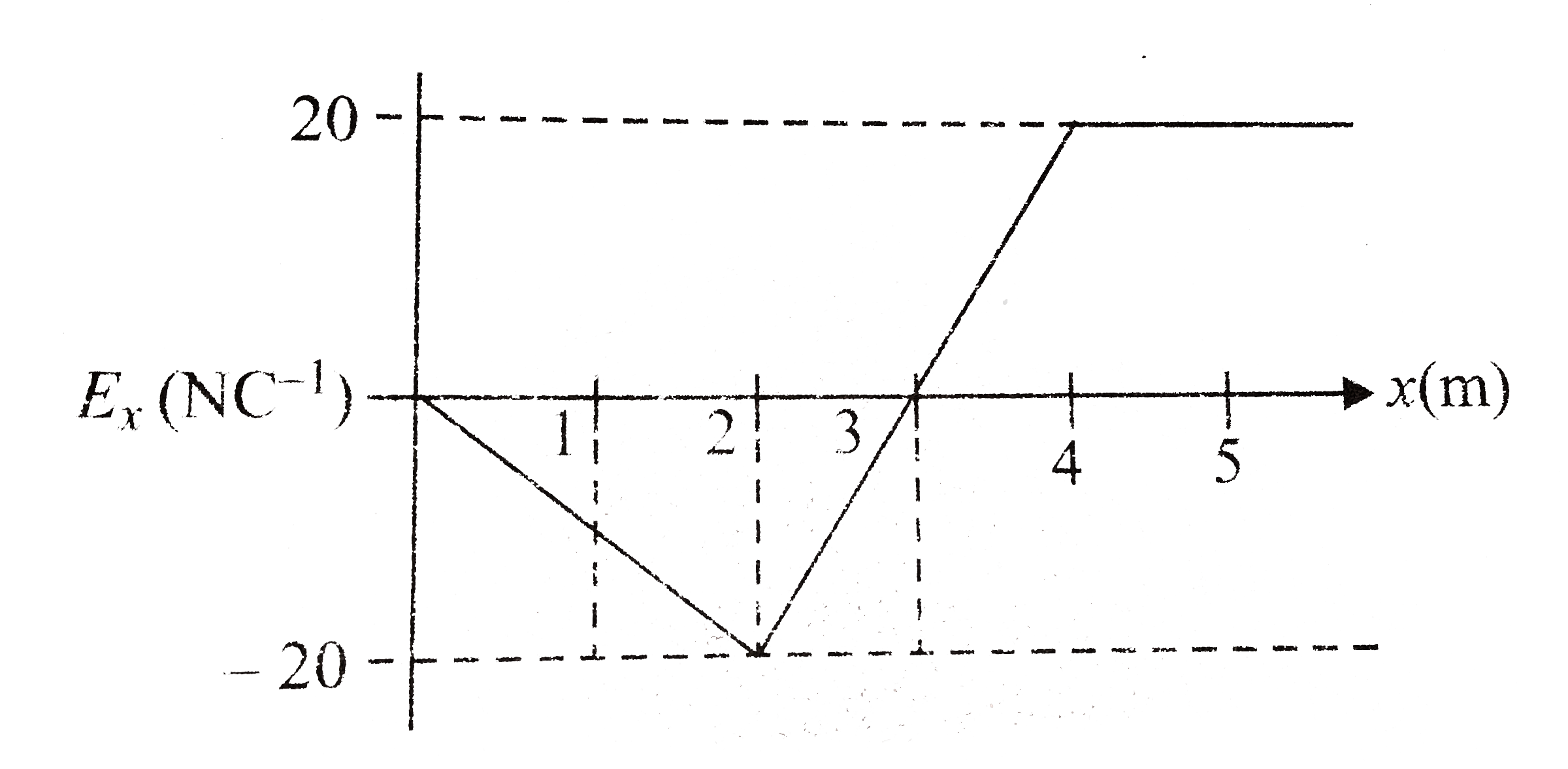
View SolutionAn electric dipole is kept in the electric field produced by a point charge
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
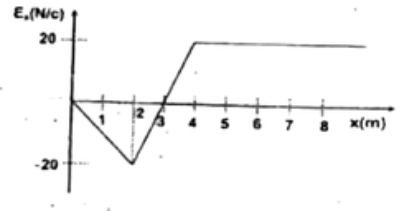
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m is
View SolutionTwo point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View Solution
