The line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC.
To prove that AD=BC in trapezium ABCD where M and N are the midpoints of the parallel sides AB and DC respectively, and the line segment MN is perpendicular to both AB and DC, we can follow these steps:
1. Identify the Given Information:
- M and N are the midpoints of sides AB and DC respectively.
- MN is perpendicular to both AB and DC.
2. Consider Triangles AMN and BMN:
- Since MN is perpendicular to AB, we have ∠AMN=90∘ and ∠BMN=90∘.
- Therefore, ∠AMN=∠BMN=90∘.
3. Use the Midpoint Property:
- Since M is the midpoint of AB, we have AM=MB.
- Since N is the midpoint of DC, we have DN=NC.
- The segment MN is common to both triangles AMN and BMN.
4. Apply the Side-Angle-Side (SAS) Congruence Criterion:
- We have:
- AM=MB (since M is the midpoint),
- MN=MN (common side),
- ∠AMN=∠BMN=90∘.
- Therefore, by the SAS criterion, △AMN≅△BMN.
5. Corresponding Parts of Congruent Triangles:
- From the congruence of triangles AMN and BMN, we have:
- AN=BN (corresponding parts).
6. Consider Triangles ADN and BNC:
- Since ∠AND=∠BNC (both are right angles),
- DN=NC (as N is the midpoint),
- AN=BN (from the previous step).
7. Apply the SAS Congruence Criterion Again:
- We have:
- AD=AD (common side),
- DN=NC (both equal),
- ∠AND=∠BNC.
- Therefore, by the SAS criterion, △ADN≅△BNC.
8. Conclude with Corresponding Parts:
- Since △ADN≅△BNC, we have AD=BC.
Conclusion:
Thus, we have proved that AD=BC.
- M and N are the midpoints of sides AB and DC respectively.
- MN is perpendicular to both AB and DC.
- Since MN is perpendicular to AB, we have ∠AMN=90∘ and ∠BMN=90∘.
- Therefore, ∠AMN=∠BMN=90∘.
- Since M is the midpoint of AB, we have AM=MB.
- Since N is the midpoint of DC, we have DN=NC.
- The segment MN is common to both triangles AMN and BMN.
- We have:
- AM=MB (since M is the midpoint),
- MN=MN (common side),
- ∠AMN=∠BMN=90∘.
- Therefore, by the SAS criterion, △AMN≅△BMN.
- From the congruence of triangles AMN and BMN, we have:
- AN=BN (corresponding parts).
6. Consider Triangles ADN and BNC:
- Since ∠AND=∠BNC (both are right angles),
- DN=NC (as N is the midpoint),
- AN=BN (from the previous step).
7. Apply the SAS Congruence Criterion Again:
- We have:
- AD=AD (common side),
- DN=NC (both equal),
- ∠AND=∠BNC.
- Therefore, by the SAS criterion, △ADN≅△BNC.
- Since △ADN≅△BNC, we have AD=BC.
Thus, we have proved that AD=BC.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- VOLUME AND SURFACE AREABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
In triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
View SolutionIn the figure AB = BC and AD is perpendicular to CD. Prove that :
AC2=2.BC.DC
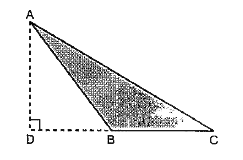
View SolutionProve that the segment joining the middle points of two non-parallel sides of a trapezium is parallel to the parallel sides and half of their sum.
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
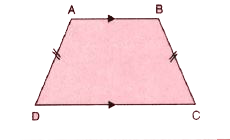
∠A=∠B
View SolutionIn a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionProve that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
View SolutionProve that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
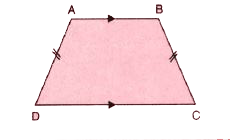
∠C=∠D
View SolutionProve that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.
View Solution
