If ABCD is a quadrilateral such that AB = AD and CB = CD , then prove that AC is the perpendicular bisector of BD.
To prove that line segment AC is the perpendicular bisector of line segment BD in quadrilateral ABCD, given that AB = AD and CB = CD, we can follow these steps:
1. Identify the Given Information:
We are given that AB = AD and CB = CD in quadrilateral ABCD.
2. Consider Triangles ABC and ADC:
We will analyze triangles ABC and ADC. Since AB = AD (given), CB = CD (given), and AC is common to both triangles, we can use the Side-Side-Side (SSS) congruence criterion.
3. Prove Triangles ABC and ADC are Congruent:
By the SSS congruence criterion:
- AB = AD
- CB = CD
- AC = AC (common side)
Therefore, triangle ABC ≅ triangle ADC.
4. Use Corresponding Parts of Congruent Triangles:
Since triangles ABC and ADC are congruent, their corresponding angles are equal:
- Let angle ACB = angle ACD (let's call these angles 1 and 2 respectively).
5. Consider Triangles AOB and AOD:
Now, we will analyze triangles AOB and AOD. We have:
- AB = AD (given)
- Angle AOB = angle AOD (from the previous step, angles 1 and 2 are equal)
- OA is common to both triangles.
6. Prove Triangles AOB and AOD are Congruent:
By the Side-Angle-Side (SAS) congruence criterion:
- AB = AD
- Angle AOB = angle AOD
- OA = OA (common side)
Therefore, triangle AOB ≅ triangle AOD.
7. Use Corresponding Parts of Congruent Triangles Again:
Since triangles AOB and AOD are congruent:
- OB = OD (let's call this length x)
- Angle AOB = angle AOD (let's call these angles 3 and 4).
8. Show that Angles 3 and 4 are Right Angles:
Since OB = OD, and angles 3 and 4 are equal, they must each be 90 degrees because they form a linear pair with the line BD. Thus:
- Angle AOB + Angle AOD = 180 degrees
- Since angle AOB = angle AOD, we have 2 * angle AOB = 180 degrees.
- Therefore, angle AOB = angle AOD = 90 degrees.
9. Repeat for Angles AOC and AOD:
Similarly, we can analyze triangles AOC and AOD. By the same reasoning, we can conclude:
- OA = OC (common side)
- Angle AOC = angle AOD = 90 degrees.
10. Conclusion:
Since AC intersects BD at point O, and we have shown that OA = OC and angles AOB and AOC are both 90 degrees, we conclude that AC is the perpendicular bisector of BD.
Final Statement:
Hence, we have proved that line segment AC is the perpendicular bisector of line segment BD.
---
We are given that AB = AD and CB = CD in quadrilateral ABCD.
We will analyze triangles ABC and ADC. Since AB = AD (given), CB = CD (given), and AC is common to both triangles, we can use the Side-Side-Side (SSS) congruence criterion.
By the SSS congruence criterion:
- AB = AD
- CB = CD
- AC = AC (common side)
Therefore, triangle ABC ≅ triangle ADC.
Since triangles ABC and ADC are congruent, their corresponding angles are equal:
- Let angle ACB = angle ACD (let's call these angles 1 and 2 respectively).
Now, we will analyze triangles AOB and AOD. We have:
- AB = AD (given)
- Angle AOB = angle AOD (from the previous step, angles 1 and 2 are equal)
- OA is common to both triangles.
By the Side-Angle-Side (SAS) congruence criterion:
- AB = AD
- Angle AOB = angle AOD
- OA = OA (common side)
Since triangles AOB and AOD are congruent:
- OB = OD (let's call this length x)
- Angle AOB = angle AOD (let's call these angles 3 and 4).
Since OB = OD, and angles 3 and 4 are equal, they must each be 90 degrees because they form a linear pair with the line BD. Thus:
- Angle AOB + Angle AOD = 180 degrees
- Since angle AOB = angle AOD, we have 2 * angle AOB = 180 degrees.
- Therefore, angle AOB = angle AOD = 90 degrees.
Similarly, we can analyze triangles AOC and AOD. By the same reasoning, we can conclude:
- OA = OC (common side)
- Angle AOC = angle AOD = 90 degrees.
Since AC intersects BD at point O, and we have shown that OA = OC and angles AOB and AOC are both 90 degrees, we conclude that AC is the perpendicular bisector of BD.
Hence, we have proved that line segment AC is the perpendicular bisector of line segment BD.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- VOLUME AND SURFACE AREABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
In a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC is perpendicular bisector of BD
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
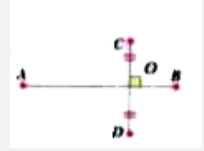
View SolutionIn the following figure is CD the perpendicular bisector of AB ?
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionIf ABCD is a cyclic quadrilateral, then prove that AC.BD=AB.CD+BC.AD
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AC=AB
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AD is parallel to BC.
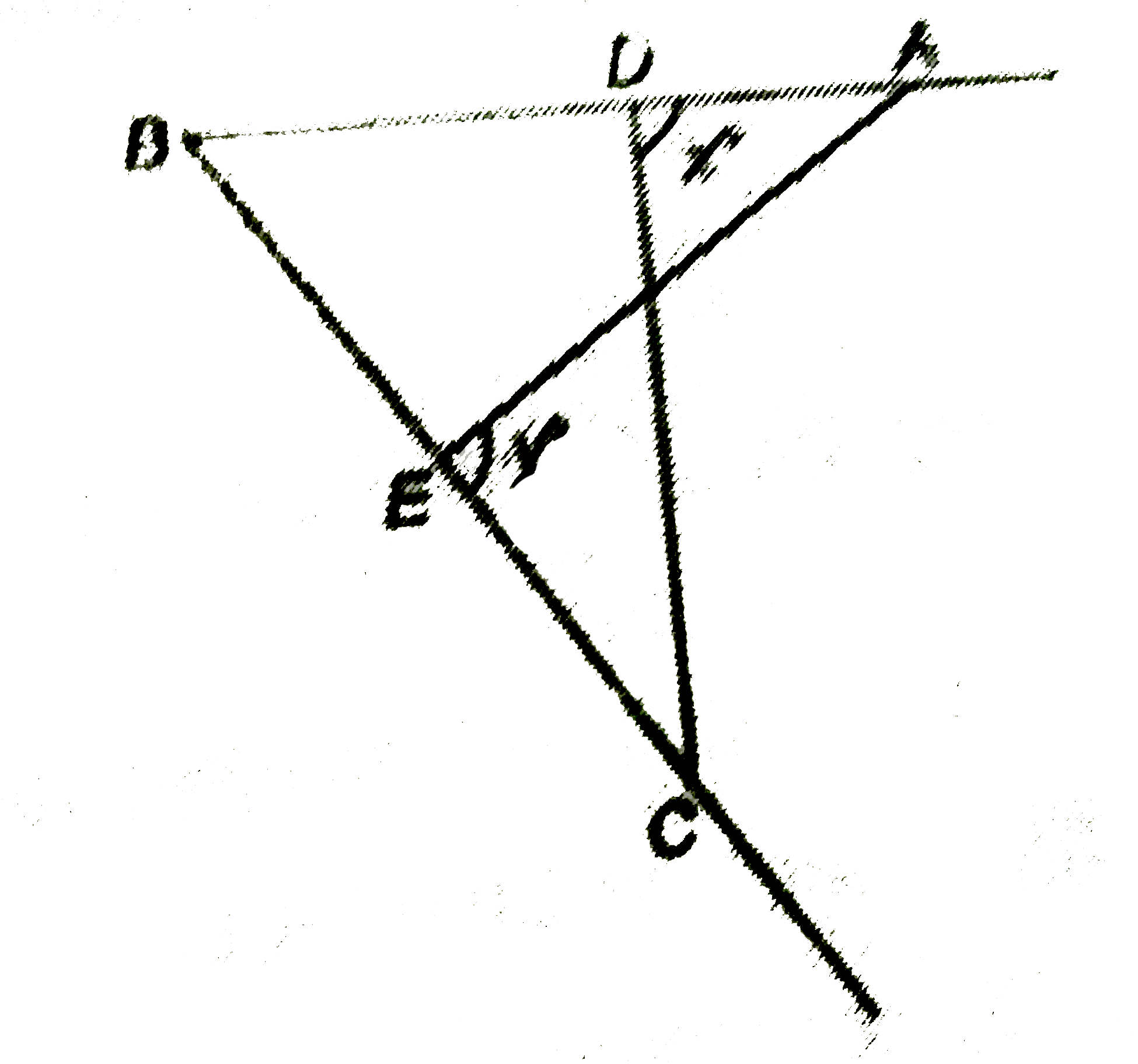
View SolutionIn the given figure, if x=y and AB=CB, then prove that AE=CD.
View Solution
