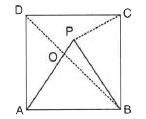
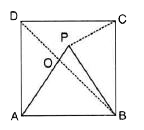
O is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle . Show that ΔOCD is an isosceles triangle .
Video Solution
Text Solution
Given O is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle .

Construction join OC and OD
To show ΔOCD is an isosceles trianlge
Proof Since,AOB is an isosceles triangle .
∴∠OAB=∠OBA=60∘
Also ∠DAB=∠CBA−∠OBA=90∘−60∘
i.e ∠DAO=∠CBO=30∘
in ΔAODandΔBOC
AO=BO [given ]
[all the side of an equilateral triangle are equal ]
∠DAO=∠CBO [proved above ]
and AD=BC [side of a square are equal ]
∴ΔAOD≅ΔBOC [by SAS congruence rule ]
Hence OD=OC [by CPCT ]
OC=OD
Hence ΔCOD is an isosceles triangle
|
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:SHORT ANSWER TYPE QUESTIONS
Explore 11 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
- VOLUME AND SURFACE AREABook:NCERT EXEMPLAR ENGLISHChapter:VOLUME AND SURFACE AREAExercise:LONG ANSWER TYPE QUESTIONS
Explore 8 Videos
Similar Questions
Knowledge Check
An equilateral triangle has three lines of symmetry, an isosceles triangle will have :
Ano line of symmetryBone line of symmetryCtwo lines of symmetryDThree lines of symmetry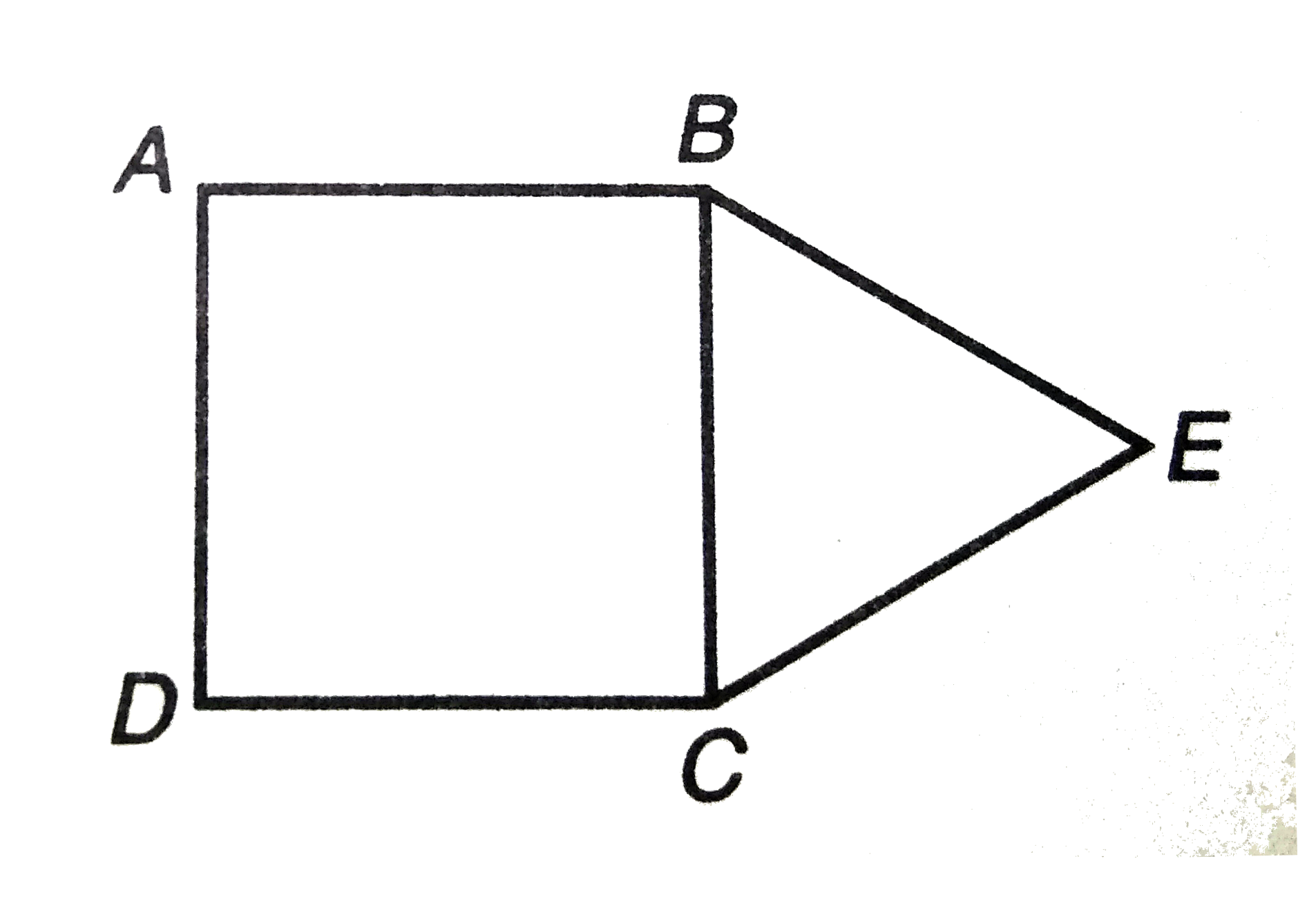
In the figure above, if the area of square ABCD is 64. What is the area equilateral triangle BEC?A8B8√3C12√3D16√3
The given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠AOB
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠BPC
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
reflex ∠APC
View SolutionThe distance between the two lines represented by the sides of an equilateral triangle a right-angled triangle an isosceles triangle
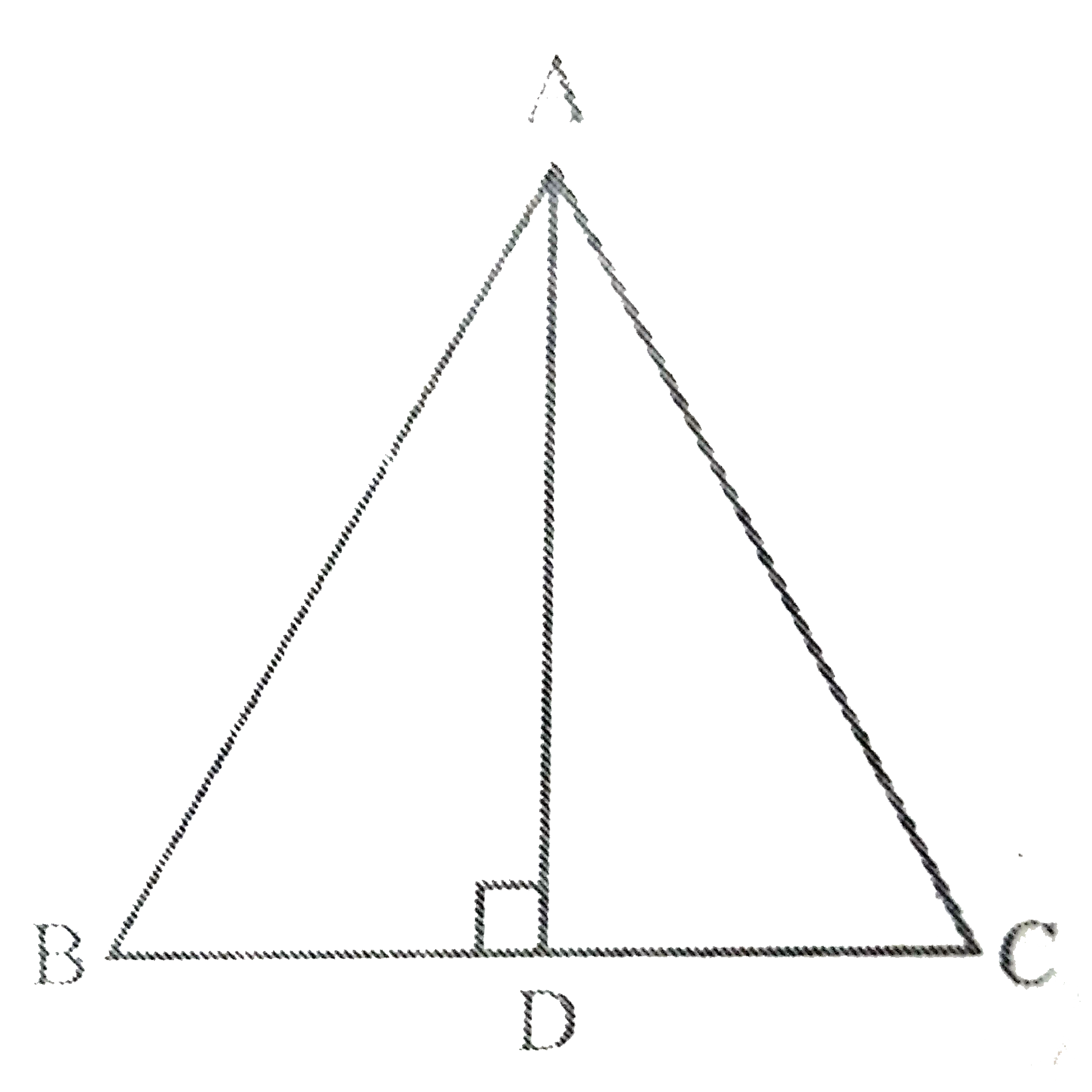
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
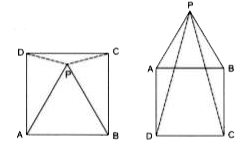
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
View Solution