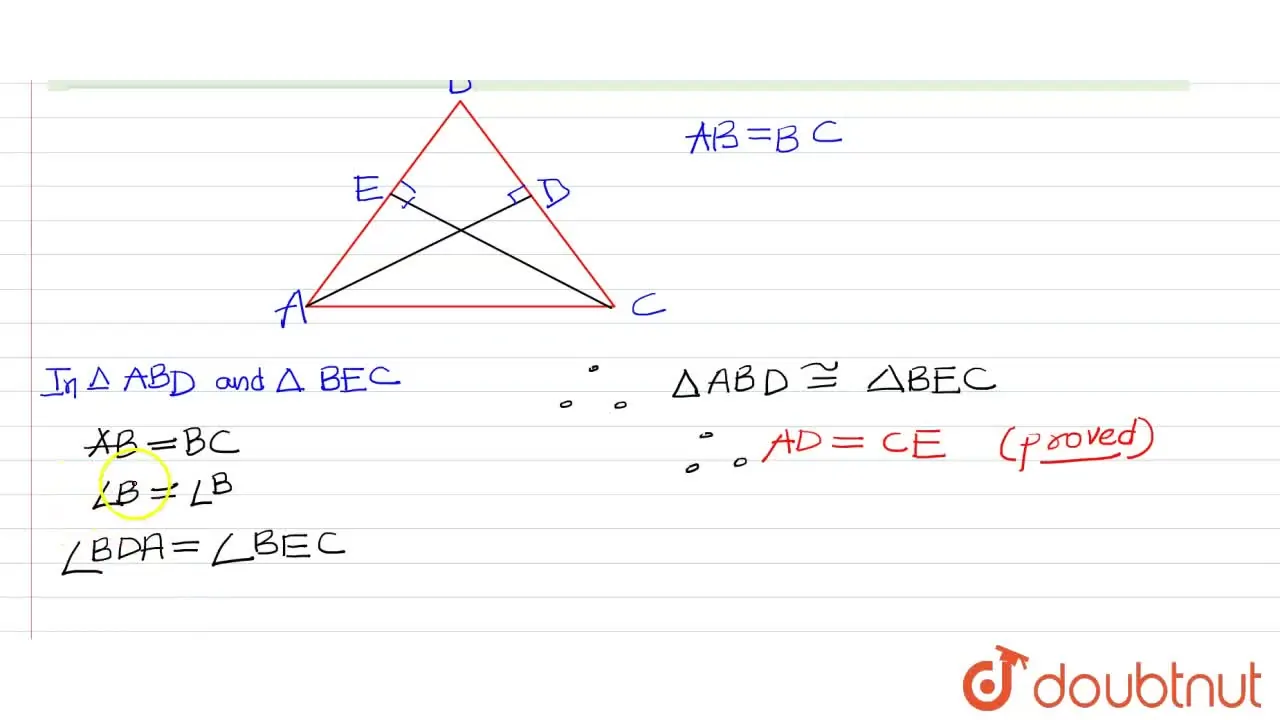
In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
Step by step video & image solution for In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS8videos
TRIANGLES
- BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS11videos
TRIANGLES
- BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS24videos
TRIANGLES
- BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)14videos
STATISTICS AND GRAPH WORK
- BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)50videos
TRIGONOMETRICAL RATIOS
Similar Questions
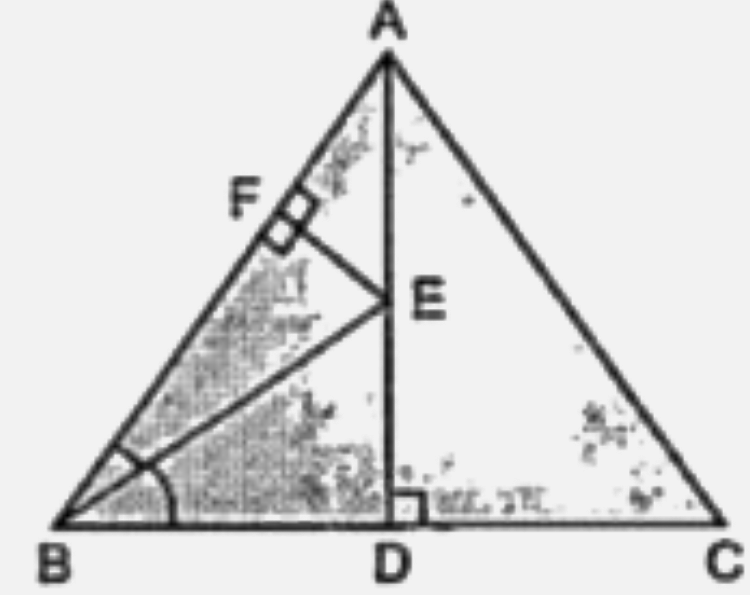
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED=EF
 View Solution
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that :
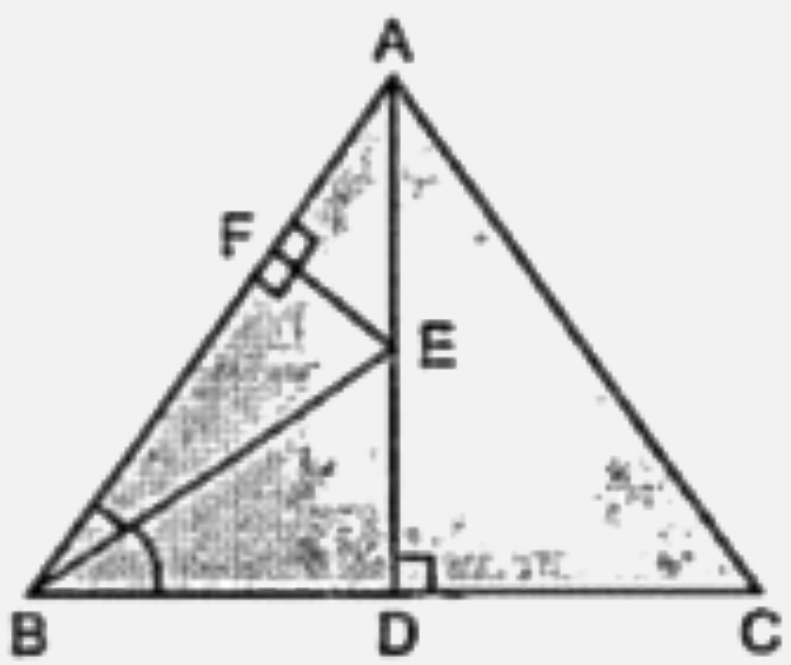
ED=EFView SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
 View Solution
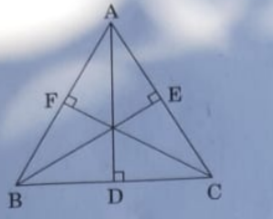
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
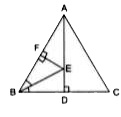 View Solution
View SolutionIn triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : AB2+AC2=2AE2+2BE2
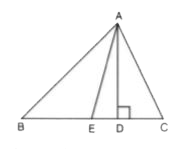 View Solution
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
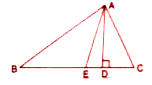 View Solution
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
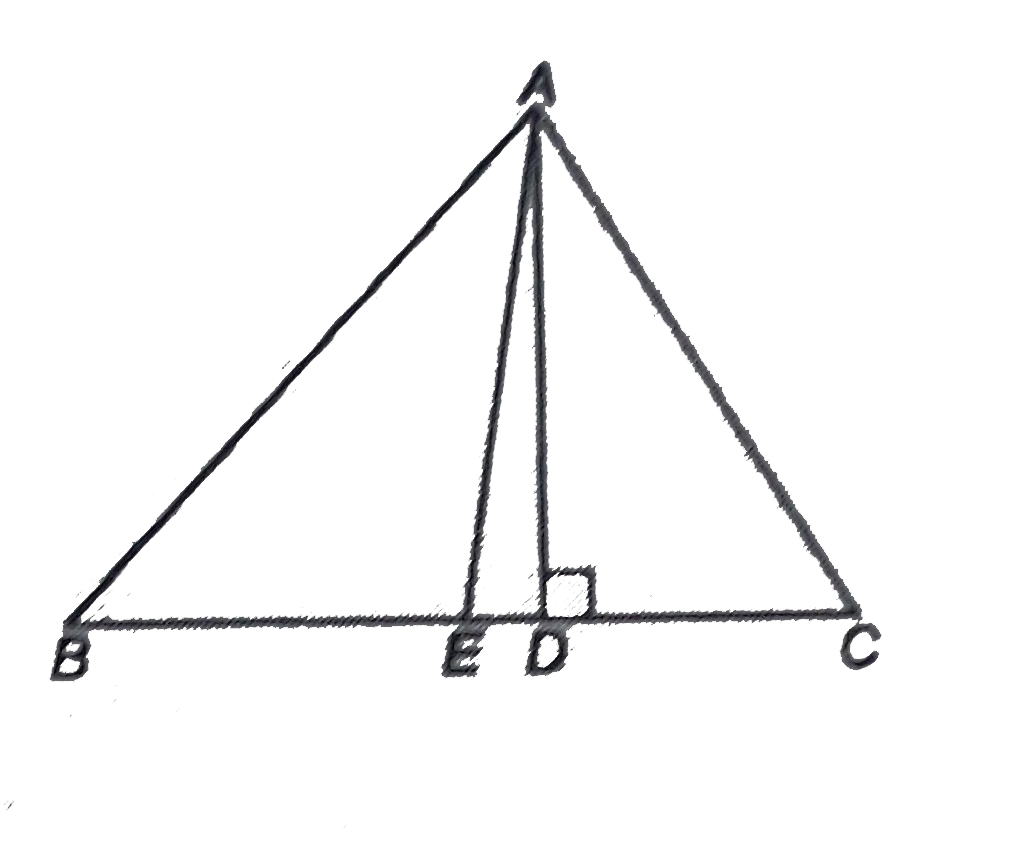 View Solution
View SolutionIn the figure AB = BC and AD is perpendicular to CD. Prove that :
AC2=2.BC.DC
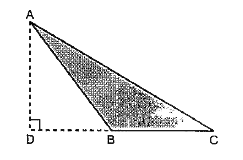 View Solution
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
 View Solution
View Solution