P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
Given In a parallelogram ABCD, P is the mid-point of DC.
To prove DA=AR and CQ=QR
Proof ABCD is a parallelogram.
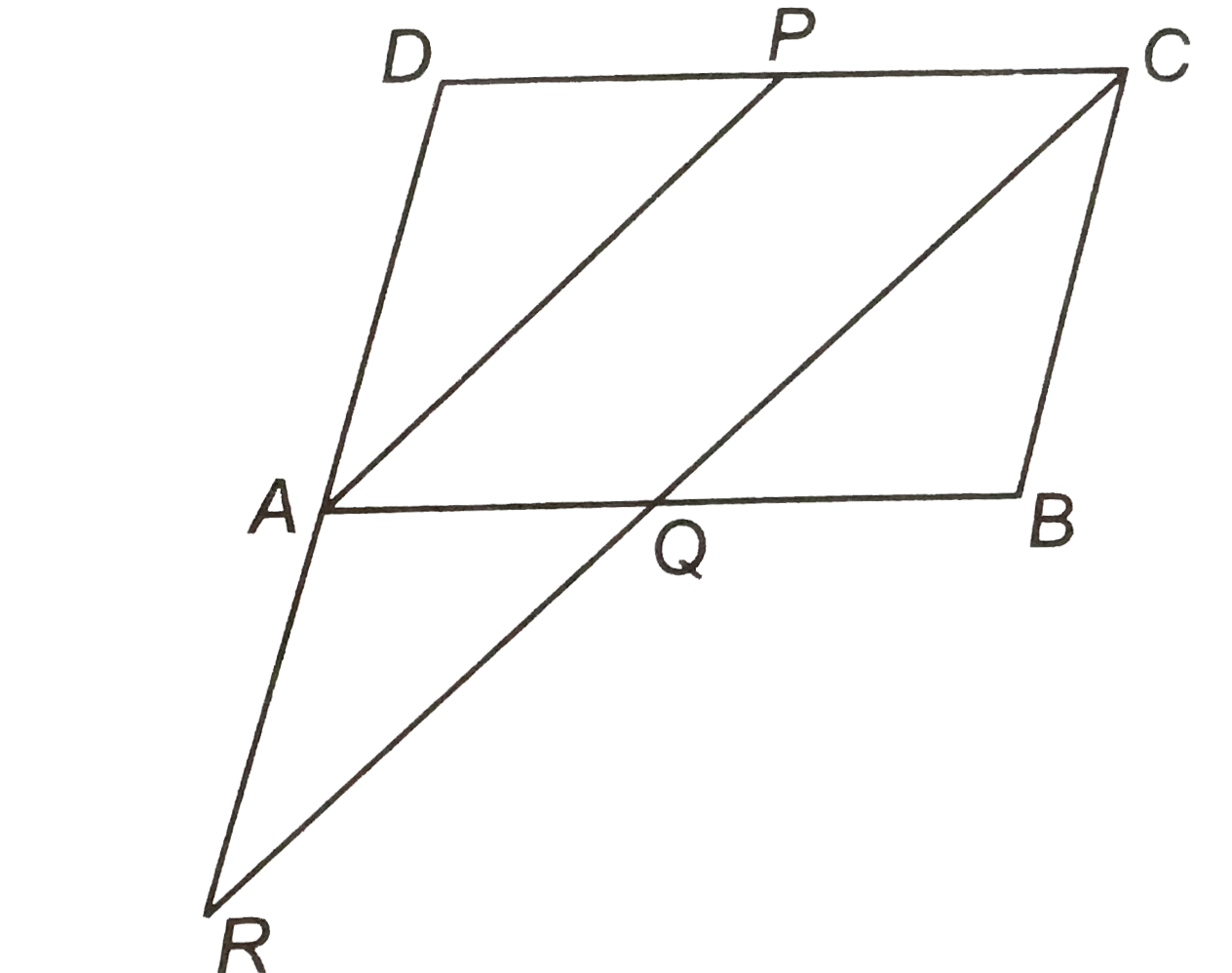
∴ BC=ADandBC∣∣AD
Also, DC=ABandDC∣∣AB
Since, P is the mid-point of DC.
∴ DP=PC=12DC
Now, QC||APandPC||AQ
So, APCQ is a parallelogram.
∴ AQ=PC=12DC
=12AB=BQ [∵DC=AB]...(i)
Now, in ΔAQR and ΔBQC, AQ=BQ [from Eq. (i)]
∠AQR=∠BQC [vertically opposite angles]
and ∠ARQ=∠BCQ [Alternate interior angles]
∴ ΔAQR≅ΔBQC [by AAS congruence rule] ltBrgt ∴ AR=BC [by CPCT rule]
But BC=DA
∴ AR=DA
Also, CQ=QR [ by CPCT rule]
Hence proved.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
P is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that:
(i) AR=2BC
(ii) BR=2 BQ
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
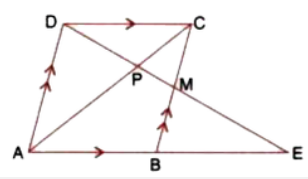
View SolutionIn the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD .
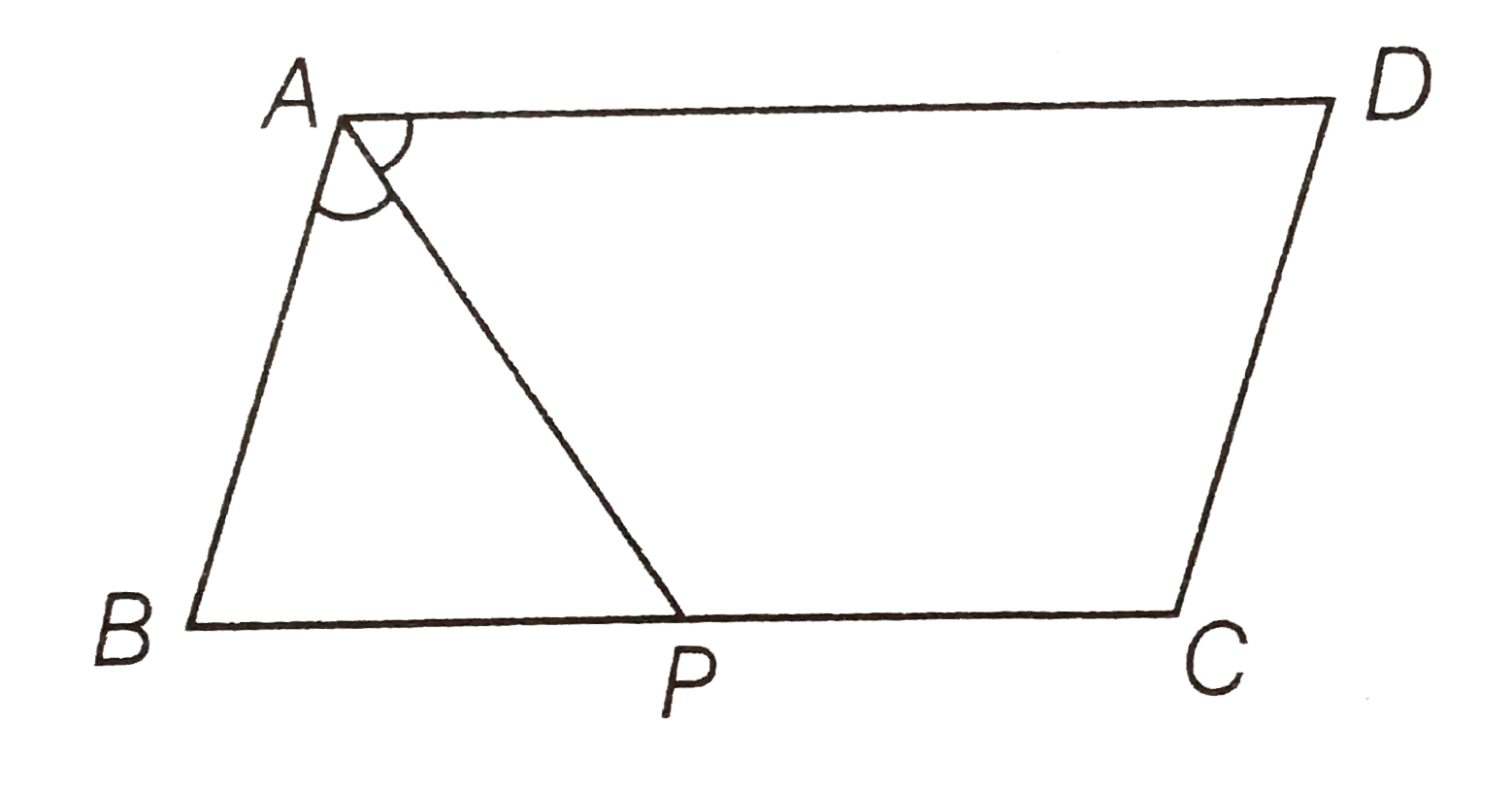
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
View Solution
