In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
To find the length of CF in the given parallelogram ABCD, we can follow these steps:
Step 1: Understand the properties of the parallelogram
In parallelogram ABCD, we know that opposite sides are equal. Therefore, AB = CD and AD = BC. Given that AB = 10 cm and AD = 6 cm, we have:
- CD = 10 cm
- BC = 6 cm
Hint: Remember that in a parallelogram, opposite sides are always equal.
Step 2: Draw the angle bisector
Draw the angle bisector of angle A, which meets side DC at point E. This means AE is the angle bisector of angle A.
Hint: The angle bisector divides the angle into two equal parts.
Step 3: Extend AE to meet BC at point F
Extend the line segment AE to meet the line extended from BC at point F.
Hint: When extending lines, ensure that you maintain the direction of the original lines.
Step 4: Identify the triangles formed
Now we have triangle AEF and triangle BCF. Since AE is the angle bisector, we can use the Angle Bisector Theorem which states that the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the lengths of the other two sides of the triangle.
Hint: The Angle Bisector Theorem is a key tool in solving problems involving angle bisectors.
Step 5: Apply the Angle Bisector Theorem
According to the Angle Bisector Theorem:
DEEC=ADAB=610=35
Let DE = 3x and EC = 5x. Then:
DE+EC=DC⟹3x+5x=10⟹8x=10⟹x=108=1.25
Thus:
DE=3x=3×1.25=3.75 cm
EC=5x=5×1.25=6.25 cm
Hint: Set up equations based on the ratios given by the Angle Bisector Theorem.
Step 6: Find CF
Since CF is equal to DE (because triangles AEF and BCF are similar), we have:
CF=DE=3.75 cm
Hint: Use the properties of similar triangles to find corresponding lengths.
Final Answer
The length of CF is 3.75 cm.
In parallelogram ABCD, we know that opposite sides are equal. Therefore, AB = CD and AD = BC. Given that AB = 10 cm and AD = 6 cm, we have:
- CD = 10 cm
- BC = 6 cm
Draw the angle bisector of angle A, which meets side DC at point E. This means AE is the angle bisector of angle A.
Extend the line segment AE to meet the line extended from BC at point F.
Now we have triangle AEF and triangle BCF. Since AE is the angle bisector, we can use the Angle Bisector Theorem which states that the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the lengths of the other two sides of the triangle.
According to the Angle Bisector Theorem:
DEEC=ADAB=610=35
Let DE = 3x and EC = 5x. Then:
DE+EC=DC⟹3x+5x=10⟹8x=10⟹x=108=1.25
Thus:
DE=3x=3×1.25=3.75 cm
EC=5x=5×1.25=6.25 cm
Since CF is equal to DE (because triangles AEF and BCF are similar), we have:
CF=DE=3.75 cm
The length of CF is 3.75 cm.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
In a parallelogram ABCD, AB= 20 cm and AD= 12cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.
View SolutionIn a parallelogram ABCD, AB=10cm, AD=6cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find the length CF.
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
Angle APB= 90∘
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line B at point X. Prove that AD = 2AB.
View SolutionIn a triangle ABC , AB = AC and ∠A=36∘ If the internal bisector of angle C meets AB at D . Prove that AD = BC.
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90∘
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
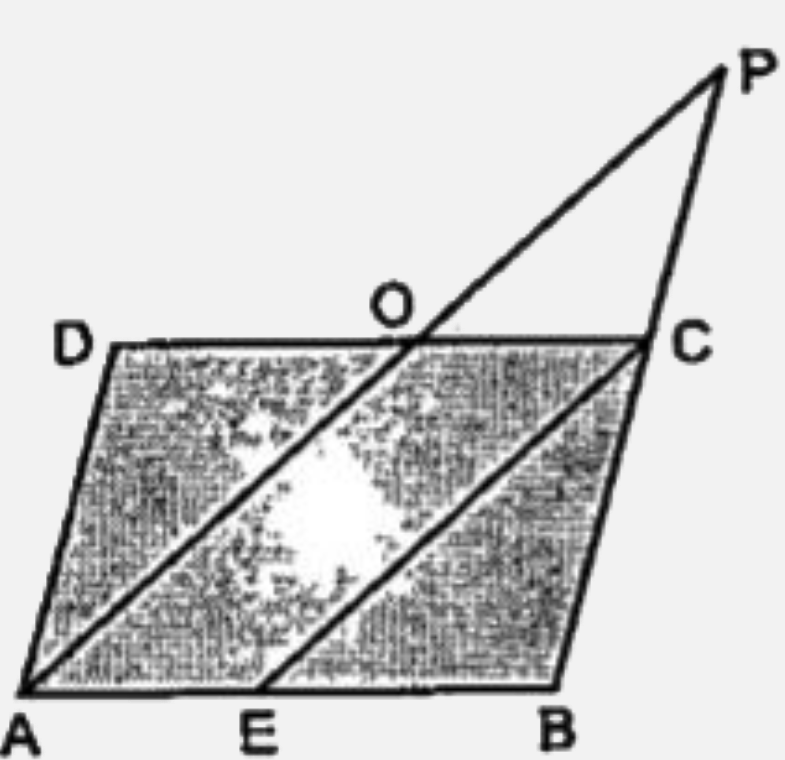
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
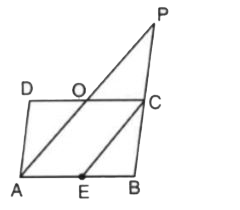
PB=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
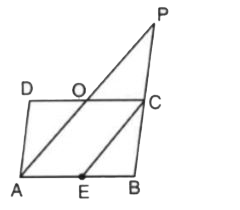
O is mid-point of AP.
View Solution
