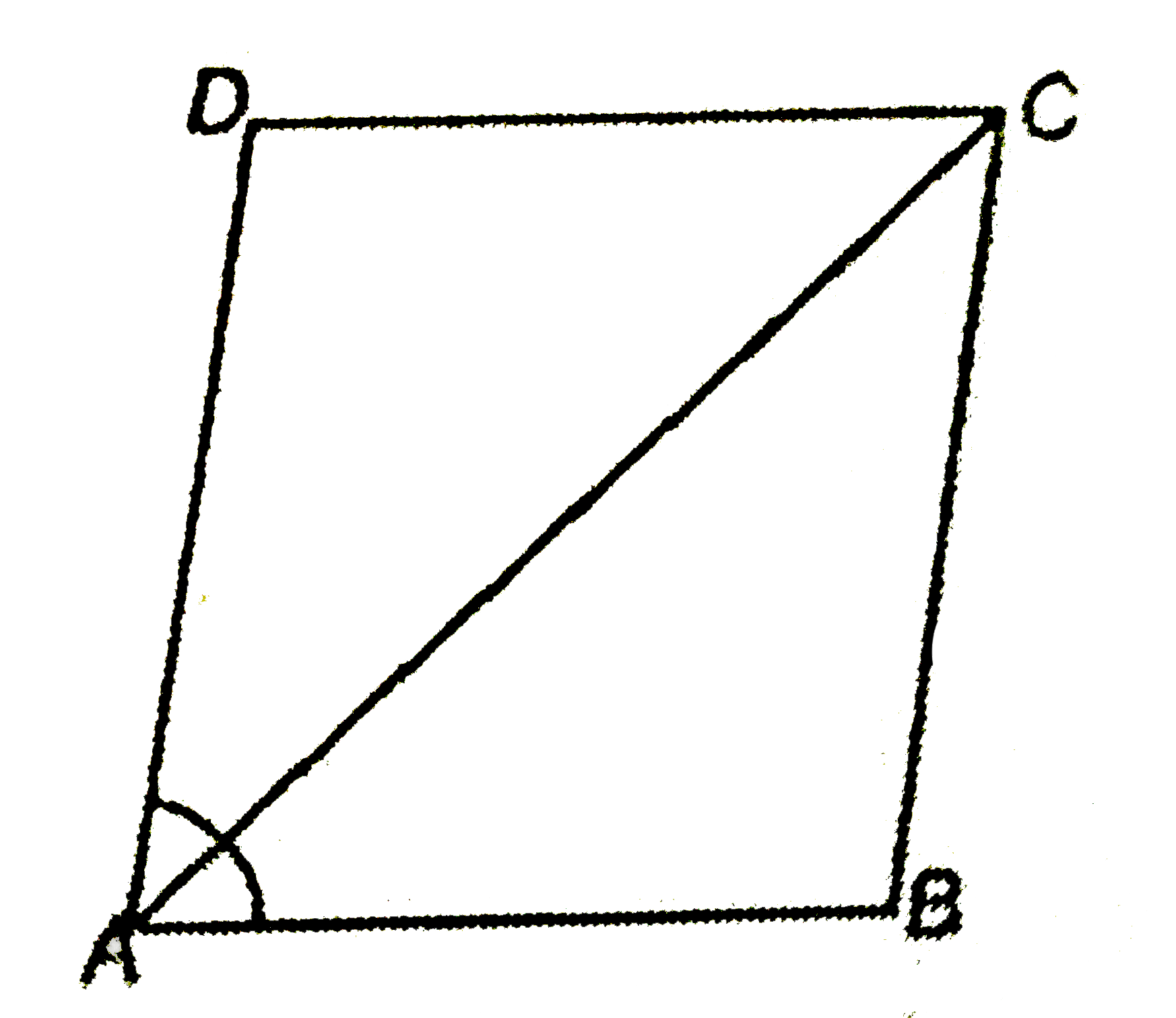
ABCD is a rectangle in which diagonal BD bisects . Show that ABCD is a square.
To prove that rectangle ABCD is a square given that diagonal BD bisects angle B, we can follow these steps:
Step 1: Draw the Rectangle
Draw rectangle ABCD with vertices A, B, C, and D such that AB is parallel to CD and AD is parallel to BC.
Step 2: Identify Angles
Since ABCD is a rectangle, we know that:
- Angle A = Angle B = Angle C = Angle D = 90 degrees.
Step 3: Understand the Given Condition
It is given that diagonal BD bisects angle B. This means:
- Let angle ABD = angle DBC = x (where x is some angle).
Step 4: Write the Angles in Terms of x
Since angle B is 90 degrees, we can write:
- Angle ABD + Angle DBC = 90 degrees
- Therefore, x + x = 90 degrees
- This implies 2x = 90 degrees, so x = 45 degrees.
Step 5: Analyze the Triangles
Now, consider triangles ABD and CBD:
- Angle ADB = 90 degrees (since it is a rectangle)
- Angle ABD = 45 degrees
- Therefore, angle ADB = 90 degrees - 45 degrees = 45 degrees.
Step 6: Show Congruence of Triangles
Now we have:
- Triangle ABD: Angle A = 90 degrees, Angle ABD = 45 degrees, Angle ADB = 45 degrees.
- Triangle CBD: Angle C = 90 degrees, Angle DBC = 45 degrees, Angle CDB = 45 degrees.
Since both triangles ABD and CBD have:
- Angle A = Angle C = 90 degrees,
- Angle ABD = Angle DBC = 45 degrees,
- Angle ADB = Angle CDB = 45 degrees,
By the Angle-Angle-Angle (AAA) criterion, triangle ABD is congruent to triangle CBD.
Step 7: Use CPCTC
From the congruence of triangles ABD and CBD, we can say:
- AB = BC (by Corresponding Parts of Congruent Triangles are Equal - CPCTC)
- Since AB = BC and AD is also equal to AB (as opposite sides of a rectangle are equal), we have:
- AB = BC = CD = AD.
Step 8: Conclude that ABCD is a Square
Since all sides of rectangle ABCD are equal (AB = BC = CD = AD), we conclude that ABCD is a square.
Final Conclusion
Thus, we have shown that if diagonal BD bisects angle B in rectangle ABCD, then ABCD must be a square.
---
Draw rectangle ABCD with vertices A, B, C, and D such that AB is parallel to CD and AD is parallel to BC.
Since ABCD is a rectangle, we know that:
- Angle A = Angle B = Angle C = Angle D = 90 degrees.
It is given that diagonal BD bisects angle B. This means:
- Let angle ABD = angle DBC = x (where x is some angle).
Since angle B is 90 degrees, we can write:
- Angle ABD + Angle DBC = 90 degrees
- Therefore, x + x = 90 degrees
- This implies 2x = 90 degrees, so x = 45 degrees.
Now, consider triangles ABD and CBD:
- Angle ADB = 90 degrees (since it is a rectangle)
- Angle ABD = 45 degrees
- Therefore, angle ADB = 90 degrees - 45 degrees = 45 degrees.
Now we have:
- Triangle ABD: Angle A = 90 degrees, Angle ABD = 45 degrees, Angle ADB = 45 degrees.
- Triangle CBD: Angle C = 90 degrees, Angle DBC = 45 degrees, Angle CDB = 45 degrees.
- Angle A = Angle C = 90 degrees,
- Angle ABD = Angle DBC = 45 degrees,
- Angle ADB = Angle CDB = 45 degrees,
From the congruence of triangles ABD and CBD, we can say:
- AB = BC (by Corresponding Parts of Congruent Triangles are Equal - CPCTC)
- Since AB = BC and AD is also equal to AB (as opposite sides of a rectangle are equal), we have:
- AB = BC = CD = AD.
Since all sides of rectangle ABCD are equal (AB = BC = CD = AD), we conclude that ABCD is a square.
Thus, we have shown that if diagonal BD bisects angle B in rectangle ABCD, then ABCD must be a square.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
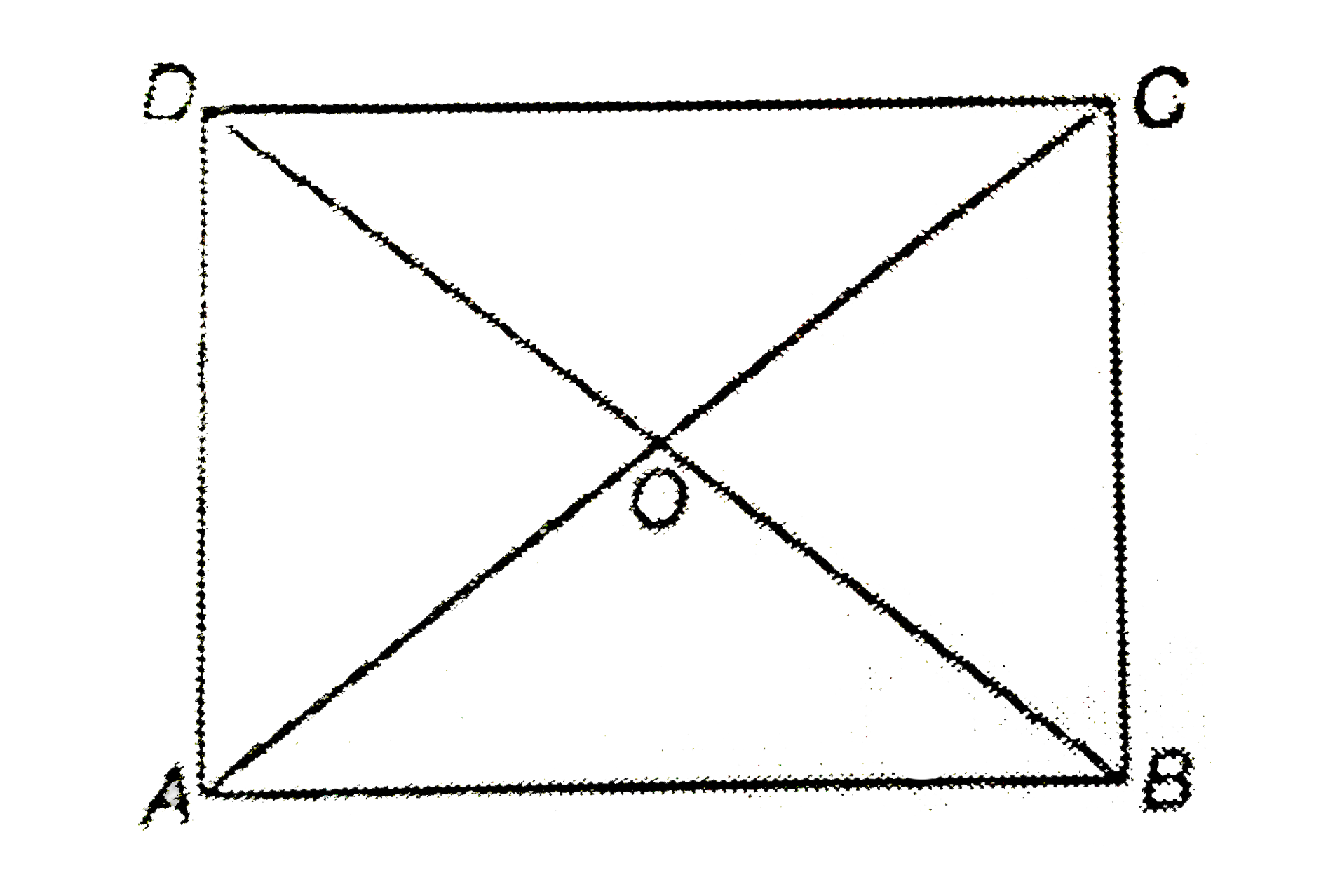
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:(i) ABCD is a square (ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
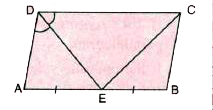
CE bisects angle C
View SolutionIn the given figure, ABCD is a rectangle, whose diagonals intersect at 'O'. Diagonal AC is produced to E and ∠DCE=145∘.
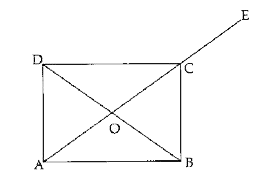
Find : (i) ∠CAB (ii) ∠AOB
View SolutionIn a parallelogram ABCD, X and Y are points on diagonal BD such that DX=BY. Prove that AXCY is a parallelogram.
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionIn a cyclic quadrilateral ABCD the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
View SolutionThe diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
View Solution
