In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
Given ABCD is a trapezium in which AB||CD. Also, E and F are respectively the mid-points of sides AD and BC.
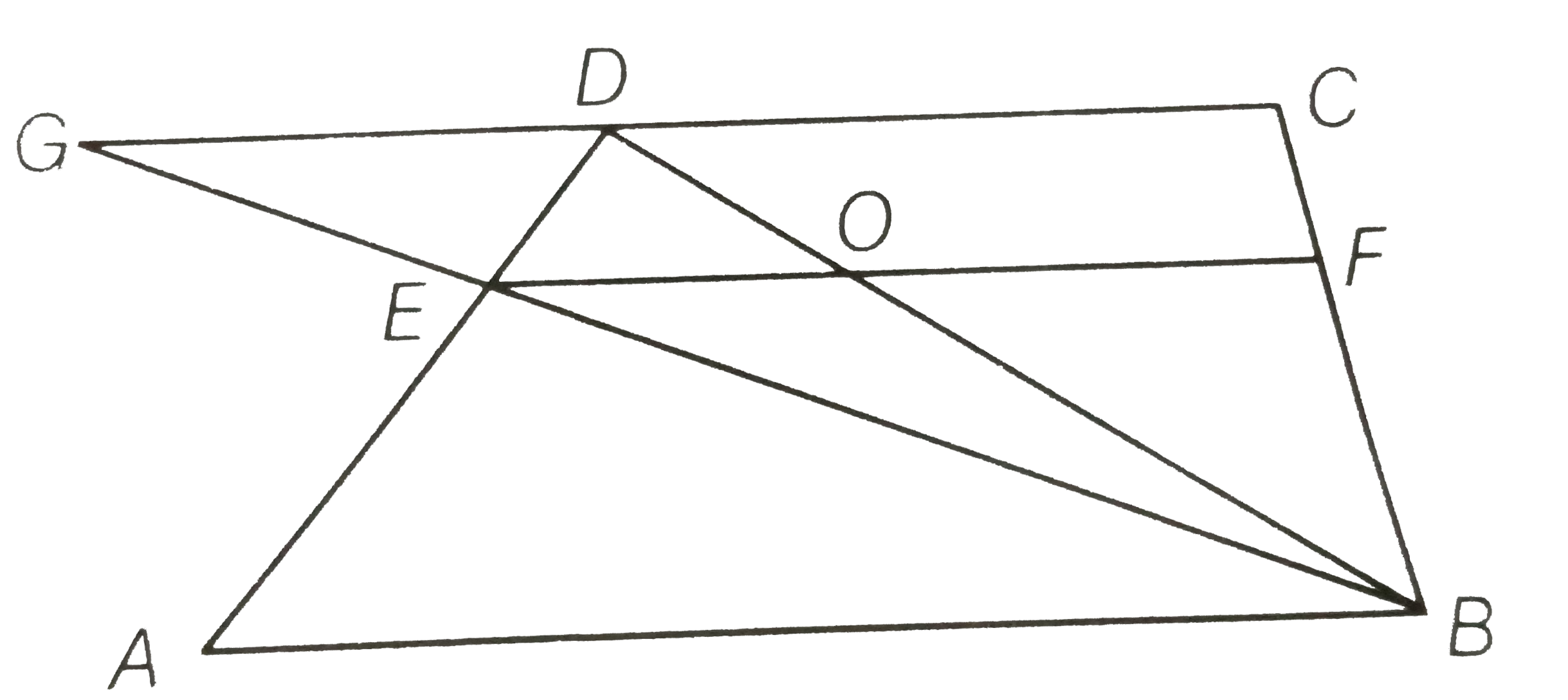
Construction Join BE and produce it to meet CD produced at G, also draw BD which intersects EF at O.
To prove EF||AB and EF =12(AB+CD).
Proof In ΔGCB, E and F are respectively the mid-points of BG and BC, then by mid-point theorem,
EF∣∣GC
But GC||ABorCD||AB [given]
∴ EF∣∣AB
In ΔADB, AB||EO and E is the mid-point of AD.
Therefore by converse of mid-point theorem, O is mid-point of BD.
Also, EO=12AB ...(i)
In ΔBDC, OF||CD and O is the mid-point of BD.
∴ OF=12CD [ by converse of mid-point theorem]...(ii)
On addillng Eqs. (i) and (ii), we get
EO+OF=12AB+12CD
⇒ EF=12(AB+CD) Hence proved.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: O is also the mid-point of BD
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of BED=14areaofABC.
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF=
View SolutionIf D is a point on the side AB of △ABC such that AD:DB=3:2 and E is a point on BC such that DE∣∣AC . Find the ratio of areas of △ABC and △BDE .
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.
View SolutionIf D is the mid-point of the side BC of a triangle ABC, prove that →AB+→AC=2→AD.
View SolutionIn △ABC,D is the mid-point of BCandED is the bisector of the ∠ADBandEF is drawn parallel to BC cutting AC in F . Prove that ∠EDF is a right angle.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points on the sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View Solution
