Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

Given Let ABCD be a parallelogram and AP, BR, CR, be are the bisectors of ∠A,∠B,∠Cand∠D, respectively.
To prove Quadrilateral PQRS is a rectangle.
Proof Since, ABCD is a parallelogram, then DC||AB and DA is a transversal.
We have, ∠A+∠D=180∘
[sum of cointerior angles of parallelogram is 180∘]
⇒ 12∠A+12∠D=90∘ [dividing both sides by 2]
⇒ ∠PAD+∠PDA=90∘ ltBrgt ⇒ ∠APD=90∘ [since, sum of all angles of a triangle is 180∘]
∴ ∠SPQ=90∘ [vertically opposite angles]
Similarly, ∠PQR=90∘
∠QRS=90∘
and ∠PSR=90∘
Thus, PQRS is a quadrilateral whose each angle is 90∘.
Hence, PQRS is a rectangle. Hence proved.
Topper's Solved these Questions
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- POLYNOMIALSBook:NCERT EXEMPLAR ENGLISHChapter:POLYNOMIALSExercise:EXERCISE 2.4 Long Answer type Questions
Explore 9 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
Similar Questions
Show that the bisectors of angles of a parallelogram form a rectangle.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View SolutionTwo parallel lines l and m are intersected by a transversal p . Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionThe angle bisectors of a parallelogram form a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View Solution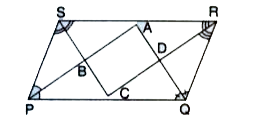
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution

