Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density p. Assume the velocity is along x-axis and to v0 is A. The drag force on the block is (where m is the mass of the gas molecule.)
Consider the digram

Let n = number of molecules per unit volume
Vrms= rms speed of the gas molecules
When block is moving with speed vo relative speed of molecules w.r.t. front face =v +vo where m = mass of molecule.
Number of collision in time Δt=12(v+vo)nΔtA, where A = area of croos- section of block and factor of 1/2 appears due to particles moving towards block.
∴ Momentum transferred in time Δt=m(v+v0)2nAΔt from front surface.
Similarly, momentum transferred in time Δt=m(v−V0)2nAΔt (from back suface)
∴Net force (drag force)=mnA[v+v0)2] [from front]
=mnA(4∨0)=(4mnAv)v0
=(4pAv)v0
Where we have assumed pmnV=mV
if v= velocity along x-axis
Then we can write KE=12mv2=12kBT
⇒ v=√kBTm ⎡⎢
⎢
⎢
⎢
⎢⎣[KB=Boltzmann constnatKE=Kinetic energyT=Temperature⎤⎥
⎥
⎥
⎥
⎥⎦
∴ From eq .(i). Drag force =(4pAv)v0=4pAv.√KBTmv0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density p. Assume the velocity is along x-axis and the are of cross-section of the block perpendicular to v0 is A. show that the drag force on the block is 4rAv0√kTm where,m is the mass of the gas molecule.
A4pAv0√kTmB2pAv0√kT3mCpA2v0√kTmDv0pA√kT2m
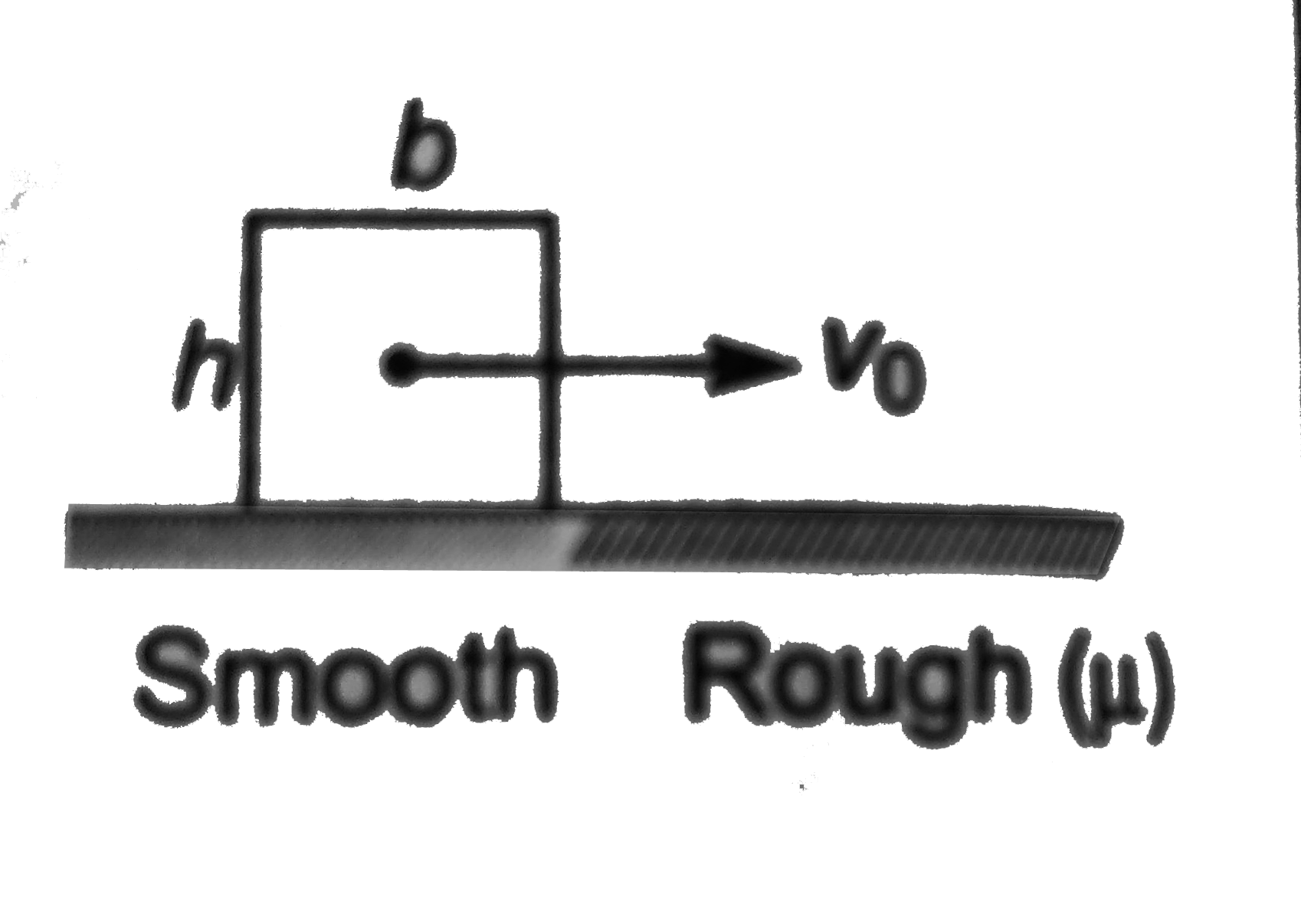
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
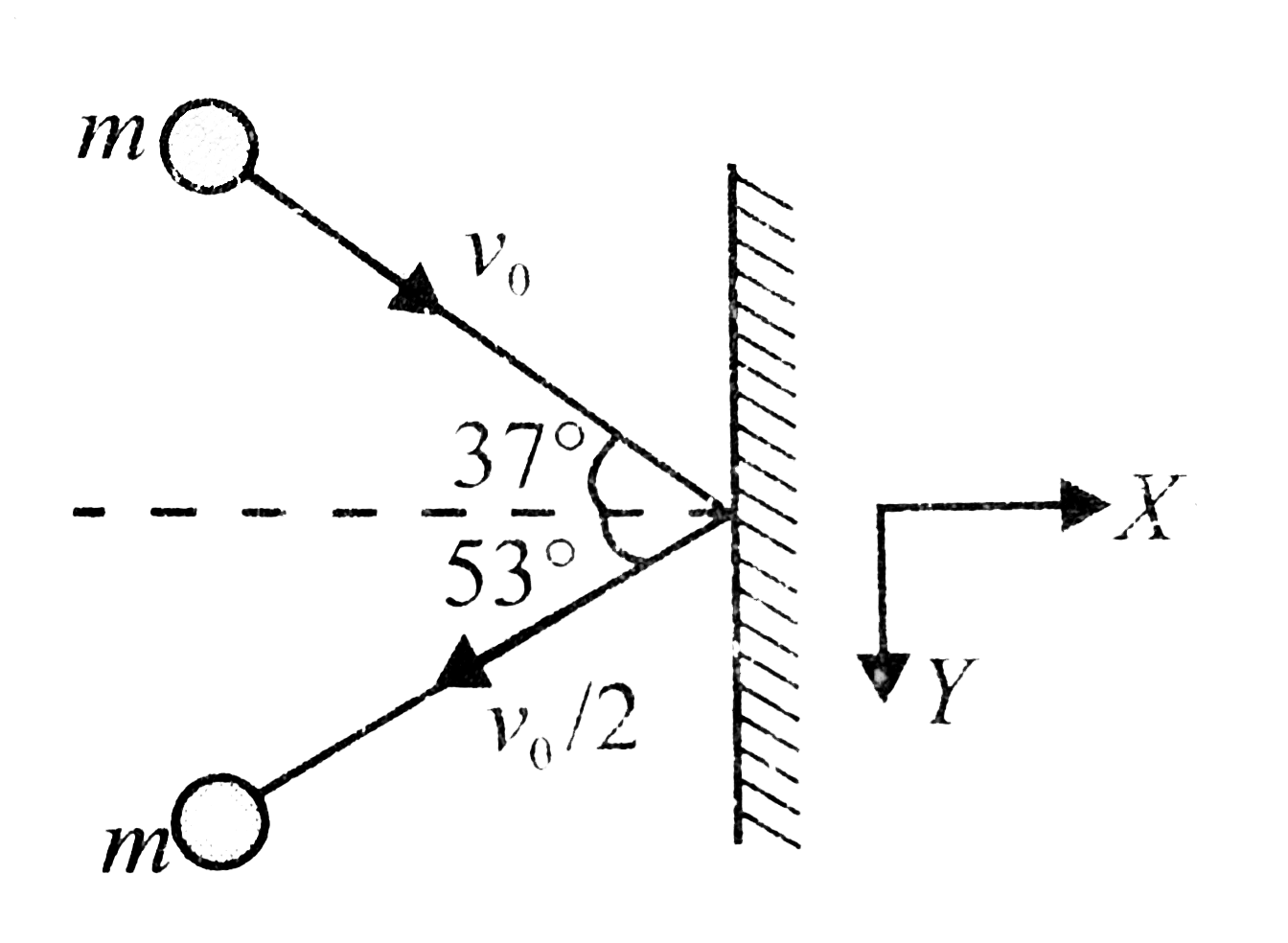
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

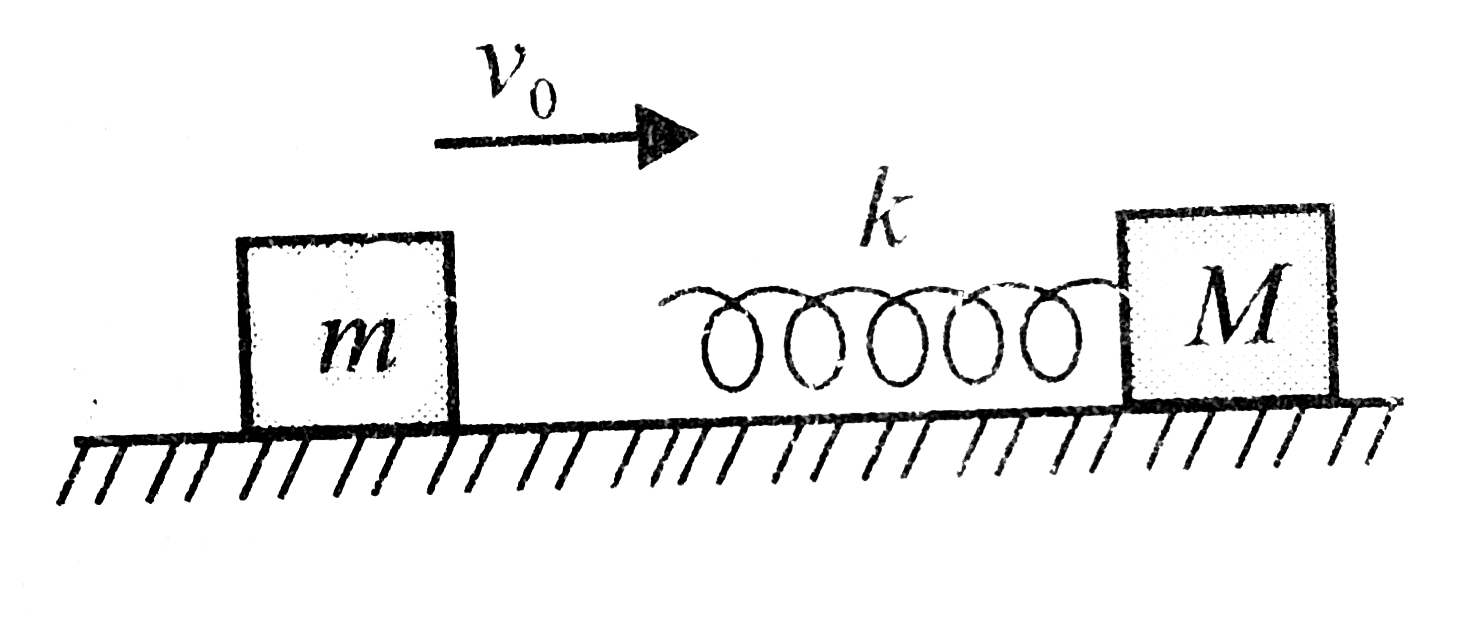
View SolutionA block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
View Solution

