A gas mixture consists of molecules of A,B and C with masses mA>mB>mC. Rank the three types of molecules in decreasing order of (a) average KE (b) rms speeds.
To solve the problem, we will analyze the average kinetic energy and the root mean square (rms) speeds of the gas molecules A, B, and C.
1. Understanding Average Kinetic Energy:
The average kinetic energy (KE) of gas molecules is given by the formula:
KE=32kT
where k is the Boltzmann constant and T is the absolute temperature.
2. Independence from Mass:
The average kinetic energy of gas molecules depends only on the temperature and is independent of the mass of the molecules. Therefore, regardless of the masses mA,mB, and mC, the average kinetic energy for all three types of molecules will be the same at a given temperature.
3. Conclusion for Part (a):
Since the average kinetic energy is the same for all types of molecules, we can rank them as:
KEA=KEB=KEC
Thus, the ranking in decreasing order of average kinetic energy is:
A=B=C
Part (b): Root Mean Square Speed
1. Understanding RMS Speed:
The root mean square speed (vrms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
2. Inversely Proportional to Mass:
From the formula, we see that the rms speed is inversely proportional to the square root of the mass of the gas molecules. Therefore, lighter molecules will have a higher rms speed compared to heavier molecules.
3. Ranking the Molecules:
Given that mA>mB>mC, we can conclude:
- vrms of molecule C (lightest) will be the highest.
- vrms of molecule B will be in the middle.
- vrms of molecule A (heaviest) will be the lowest.
Thus, the ranking in decreasing order of rms speeds is:
vrms,C>vrms,B>vrms,A
Final Answers:
- (a) Average KE: A=B=C
- (b) RMS Speeds: C>B>A
The average kinetic energy (KE) of gas molecules is given by the formula:
KE=32kT
where k is the Boltzmann constant and T is the absolute temperature.
The average kinetic energy of gas molecules depends only on the temperature and is independent of the mass of the molecules. Therefore, regardless of the masses mA,mB, and mC, the average kinetic energy for all three types of molecules will be the same at a given temperature.
Since the average kinetic energy is the same for all types of molecules, we can rank them as:
KEA=KEB=KEC
Thus, the ranking in decreasing order of average kinetic energy is:
A=B=C
The root mean square speed (vrms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
From the formula, we see that the rms speed is inversely proportional to the square root of the mass of the gas molecules. Therefore, lighter molecules will have a higher rms speed compared to heavier molecules.
Given that mA>mB>mC, we can conclude:
- vrms of molecule C (lightest) will be the highest.
- vrms of molecule B will be in the middle.
- vrms of molecule A (heaviest) will be the lowest.
vrms,C>vrms,B>vrms,A
- (a) Average KE: A=B=C
- (b) RMS Speeds: C>B>A
Topper's Solved these Questions
Similar Questions
Five molecules of a gas have speeds 1, 1, 3, 3, 2 km/s the value of the r.m.s spreed of the gas molecules is
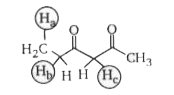
View SolutionRank the hydrogen atoms (Ha,Hb,Hc) present in the following molecule in decreasing order of their acidic strength.
View SolutionThe rms speed of oxygen molecule in a gas at 27∘C would be given by
View SolutionThe average velocity of molecules of a gas of molecular weight (M) at temperature (T) is
View SolutionThe mass of molecule A is twice the mass of molecule B. The rms speed of A is twice the rms speed of B. If two samples of A and B contain same number of molecules. If the pressure of gas B is 2atm then what will be the pressure of gas A ( atm) . If two samplest are taken in separate containers of equal volume ?
View SolutionFigure shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find the

(a) acceleration of each block
(b) tension in the string
(c ) force exerted by m1 on m2. ltbr> (d) force exerted by m2 on the incline.
View SolutionConsidering all type of D.O.F for HCl molecule of mass m having Vrms as ¯v. Then the temperature of gas will be
View SolutionThe most probable velocity of the molecules of a gas is 1 km/sec. The R.M.S velocity of the molecules is
View SolutionThree closed vessels A,B and C are at the same temperature T and contain gases which obey the Maxwellian distribution of velocities. Vessel A contains only O2,B only N2 and C a mixture of equal quantities of O2 and N2. If the average speed of the O2 molecules in vessel A is V1, that of the N2 molecules in vessel B is V2, the average speed of the O2 molecules in vessel C is (where M is the mass of an oxygen molecules)
View SolutionAir consists mainly of nitrogen and oxygen molecules. Relative molecular masses of nitrogen and oxygen are 28 and 32 respectiely. Calculate :
(i) the ratio of the rms speed of nitrogen molecules to that of the oxygen molecules in air and
(ii) the ratio of the r.m.s. speed of oxygen molecules in air at 0∘C to that at 10∘C.
View Solution
