As shown in the figure, AB and CD are two common tangents to circles with centres O1andO2 and different radius. Prove that AB=CD 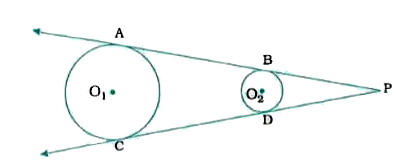 Solution in Gujrati
Solution in Gujrati
Here sources A, B, C, D emit coherent light waves simultaneously with amplitude a, wavelength λ and frequency f. When these waves superpose at point R1 at time t, displacements of light vectors in them are suppose yA,yB,yCandyD respectively.
Now according to wave equation y=asin(ωt−kx+ϕ) for simplicity assume (ωt−kx)=θ and initial phase for source A as ϕ=0. Now
yA=asin(θ+0)=asinθ ......(1)
(ii) Here BR1−AR1=λ2 and so, at point R1 at time t, phase of B will be less than phase of A by amount π rad and so,
yB=asin(θ−π)=asin{−(π−θ)}
=−asin(π−θ)
∴yB=−asinθ ....(2)
Here CR1−AR1=λ2+λ2=λ and so at point R1, at time t phase of C is less then phase of A by amount 2π rad and so,
yC=asin(θ−2π)=asin{−(2π−θ)}
=−asin(2π−θ)
∴yC=−a(−sinθ)=asinθ ......(3)
(iv) Here DR21=DB2+BR21
=(λ2)2+d2
∴DR1=√d2+λ24
Path difference betwen D and A
=DR1−AR1
=DR1−(BR1−AR1)
=√d2+λ24−(d−λ2)
=√d2+λ24−d+λ2
={d2(1+λ24d2)}1/2−d+λ2
=d(1+λ24d2)1/2−d+λ2
=d(1+λ28d2)−d+λ2
(Expanding according to binomial theorem and then retaining only first two terms)
=d(1+0)−d+(λ)(2)(∴Hered>>>>λ)
=λ2
⇒ At point R1, at time t, phase of D would be less than phase of A by amount π rad. Hence,
yD=asin(θ−π)
=asin{−(π−θ)}
=−asin(π−θ)
∴yD=−asinθ ......(4)
Now, resultant displacement of light vector at point R1 at time t,
y=yA+yB+yC+yD
=asinθ−asinθ+asinθ−asinθ
∴y=0
⇒ Now, resultant intensity of light at point R1, IR1=0 ....(5)
Now, let us consider point R2,
(i) Path difference between A and B,
=AR2−BR2
=√d2+λ24−d
={d2(1+λ24d2)}1/2−d
=d(1+λ24d2)1/2−d
=d(1+λ24d2)1/2−d
=d+λ28d−d
=λ28d
≈0 (∴d>>>>λ)
If, y.A=asinθ then y.A=asinθ
( ∴ path differene =0 )
similarly y.C=asinθ
( ∴ path difference =0)
But yD=asin(θ−π)
( ∴ path difference =λ2 )
=asinθ{−(π−θ)}
=−asin(π−θ)
=−asinθ
Now, resultant displacement of light vector at point R2 at time t is
y.=yA+y.B+y.C+y.D
=asinθ+asinθ+asinθ−asinθ
=2asinθ
=2asin(ωt−kx) (∴θ=ωt−kx)
Now, if instantaneous intensity of light at point R2 at time t is I then,
1∝y.2
∴I∝4a2sin2(ωt−kx)
∴I=K×4a2sin2(ωt−kx)
⇒ Average intensity of light in every periodic time) at point R2 will be,
∴<I>=K×4a2×12=2Ka2
⇒ Now, showing above average intensity at point R1 by symbol IR2,
IR1=2Ka2 ......(6)
From equation (5) and (6), IR2>IR1
If all the sources are switched on at a time then intensity of light at point R2 will be greater than that at point R1.
(ii) Now, when source B is turned off, resultant displacement of light vector at point R1,
y=yA+yC+yD
=asinθ+asinθ−asinθ
(From equations (1), (2), (4))
=asinθ
y=asin(ωt−kx)
∴IR1=K×a2×12=Ka22 ......(7)
Now, resultant displacement of light vector at point R2 will be,
y.=y.A+y.C+y.D
∴y.=asinθ+asinθ−asinθ
∴y.=asinθ
∴y.=asin(ωt−kx) ,
∴IR2=K×a2×12=Ka22 .....(8)
From equations (7) and (8) IR1=IR2 ......(9)
When source B is turned off, intensities of light at points R1 and R2 would be equal.
(iii) Now, when source D is turned off, resultan displacement of light vector at point R1 is
y=yA+yB+yC
∴y=asinθ−asinθ+asinθ
(From equations (1), (2), (3))
∴y=asinθ
∴y=asin(ωt−kx)
∴IR1=K×a2×12=Ka22 ......(10)
Here, resultant displacement of light vector at point R2 will be
y.=y.A+y.B+y.C
∴y.=asinθ+asinθ+asinθ
∴y.=3asinθ
∴y.=3asin(ωt−kx)
∴IR2=K×9a2×12=9Ka22 .....(11)
From equations (10) and (11), IR2>IR1
Intensity of light at point R2 will be greater than that at point R1.
(iv) Here, whether we turn off B or we turn off D in both the cases same intensity of light is obtained at point R1. Hence receiver R1 can not differentiate (or can not distinguish) betweeen these two phenomena.
But receiver R2 can distinguish between these two phenomena because according to equation (6), when all the four sources are turned "on" intensity of light at point R2 is 2Ka2. Now, when only B is turned "off", intensity of light at point R2 decreases and becomes 12Ka2 (as per equation (7) and when only D is turned "off" intensity of light at point R2, increases and becomes 9Ka22.
Thus, when intensity of light decreases at point R2, it will come to know that source B is turned "off" and when intensity of light increases at point R2, it will come to know that source D is turned "off".
Topper's Solved these Questions
- WAVE OPTICSBOOK - KUMAR PRAKASHANCHAPTER - WAVE OPTICSEXERCISE - SECTION-D (MULTIPLCE CHOICE QUESTIONS (MCQS)) (MCQS FROM DARPAN BASED ON TEXTBOOK)
239 Videos
- WAVE OPTICSBOOK - KUMAR PRAKASHANCHAPTER - WAVE OPTICSEXERCISE - SECTION-C NCERT Exemplar Solution (Short Answer Type Questions )
3 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-D : Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams)
129 Videos
Similar Questions
According to particle theory of light what is the velocity of light in a dense medium, compared to that in rare medium ?
View SolutionCan reflection result in plane polarised light if the light is incident on the interface from the side with higher refractive index ?
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionCommon tangents AB and CD to two circles intersects at E.Prove that AB=CD
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

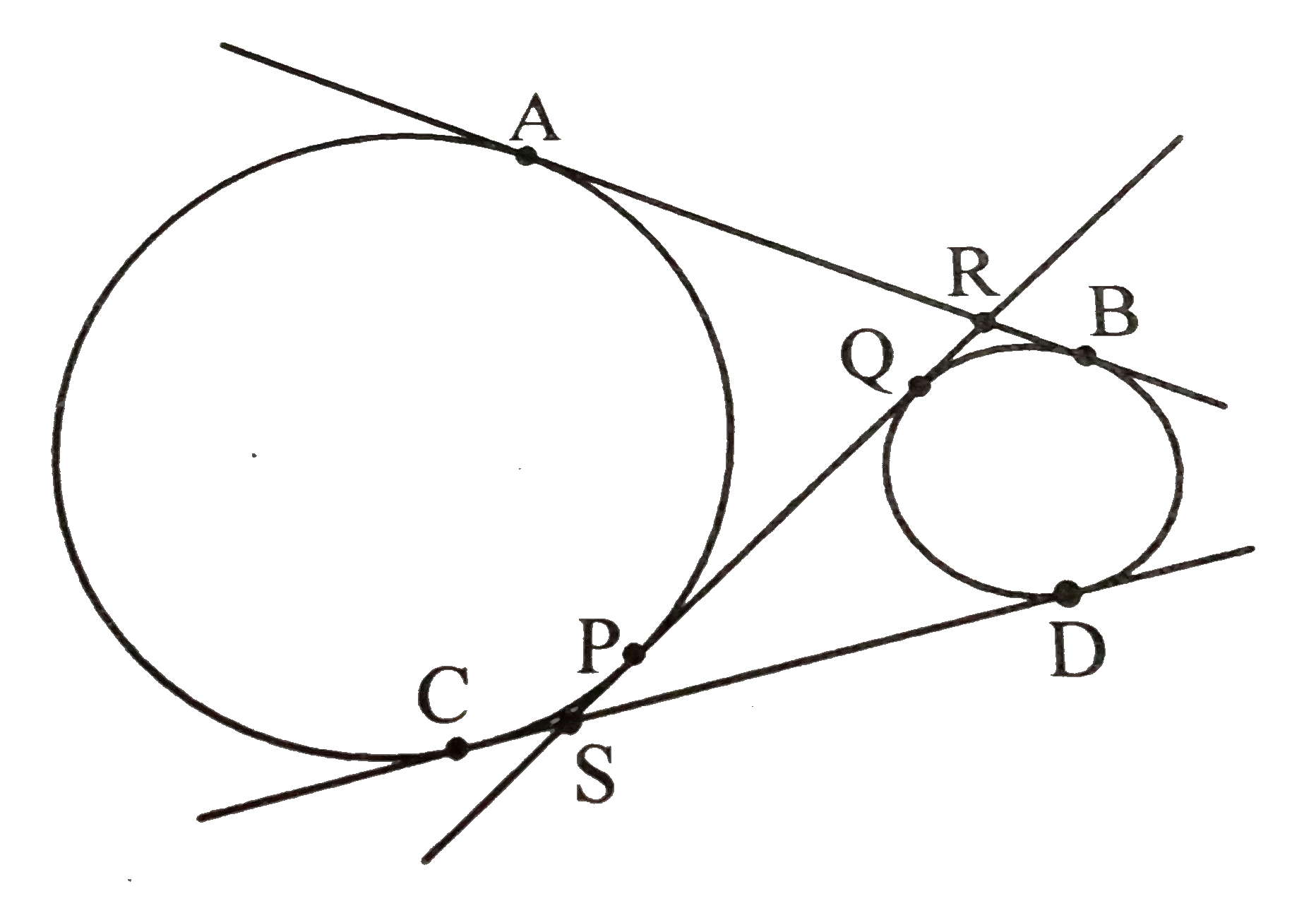
View SolutionSuppose S1 and S2 are two unequal circles, AB and CD are the direct common tangents to these circles. A transverse common tangent PQ cuts AB in R and CD in S. If AB = 10, then RS is -
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View Solutionचित्र में, AB और CD दो वृतों की उभयनिष्ठ स्पर्श रेखाएँ परस्पर बिन्दु E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AE+ED=BE+EC.
View Solutionसंलग्न चित्र में, दो वृत्तों की उभयनिष्ठ स्पर्श रेखायें AB और CD एक-दूसरे को P पर प्रतिच्छेद करती है। सिद्ध कीजिए कि AB=CD.

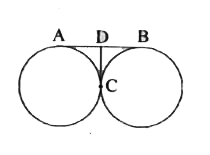
View Solutionदिए गए चित्र में AB और CD परस्पर स्पर्श करने वाले वृतो की दो स्पर्श रेखाएं है। यदि CD=3 सेमी है तो AB की लम्बाई है -
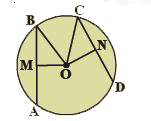
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
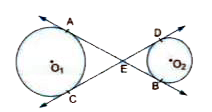
View SolutionAB and CD are common tangents to two circles which intersect each other at C as shown in the figure IF AB = 6cm , find CD.

View Solution
