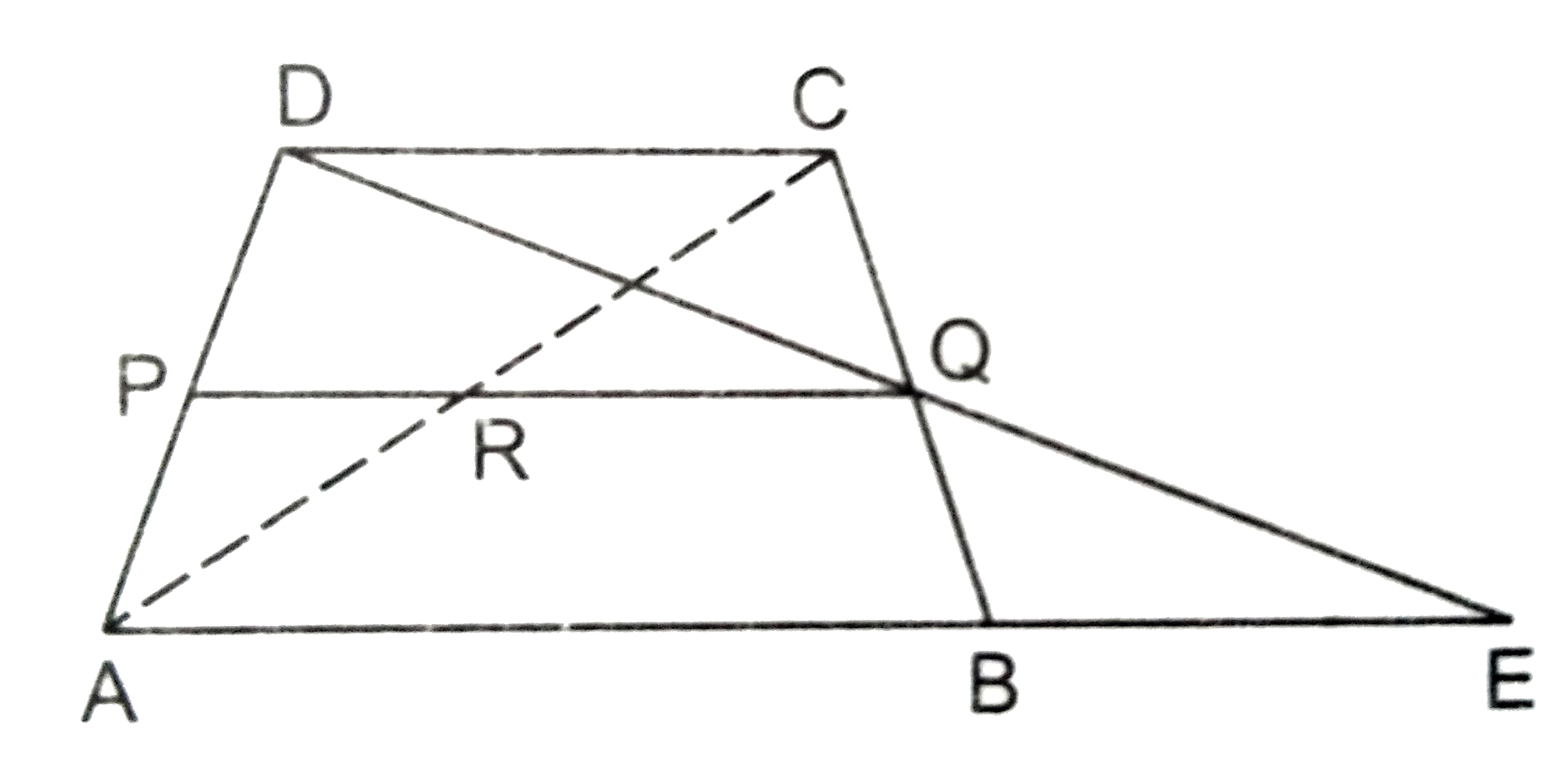
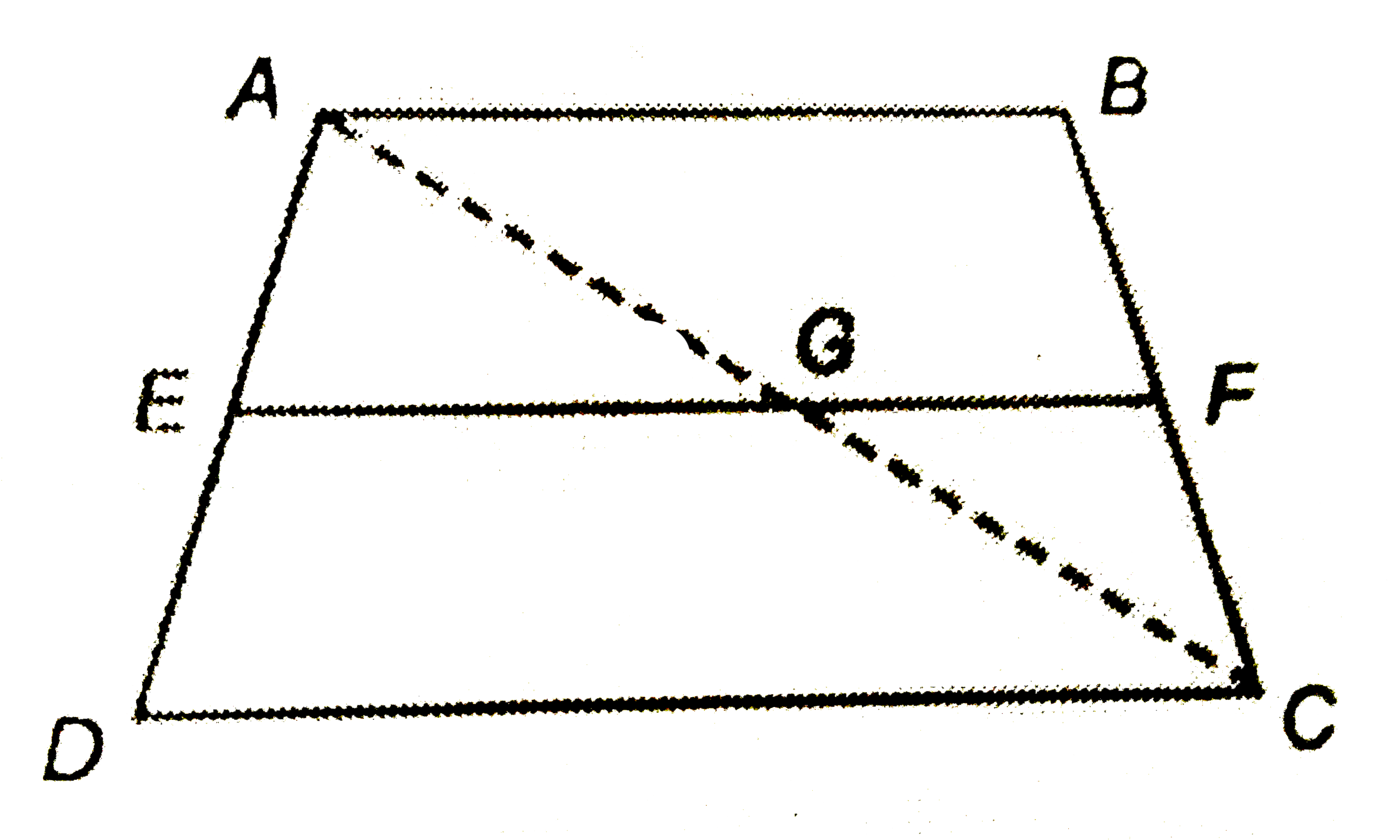
In the adjoining figure, ABCD is a trapezium in which AB||DC and P, Q are the midpoints of AD and BC respectively. DQ and AB when produced meet at E. Also, AC and PQ intersect at R. Prove that (i) DQ = QE, (ii) PR||AB and (iii) AR = RC.
Video Solution
Text Solution
△QCD≅△QBE. So, DQ=QE.
PQ||AE ⇒ PQ||AB||DC||⇒ AB||PR||DC.
Now, AB||PR||DC are cut by AD and AC. Use intercept theorem.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 47 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 9 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
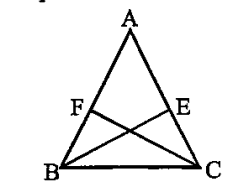 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
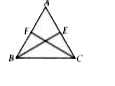 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
In the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
diagonal AC = diagonal BD

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠A=∠B

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D

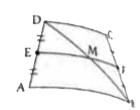
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
ΔABC≈ΔBAD

View Solution