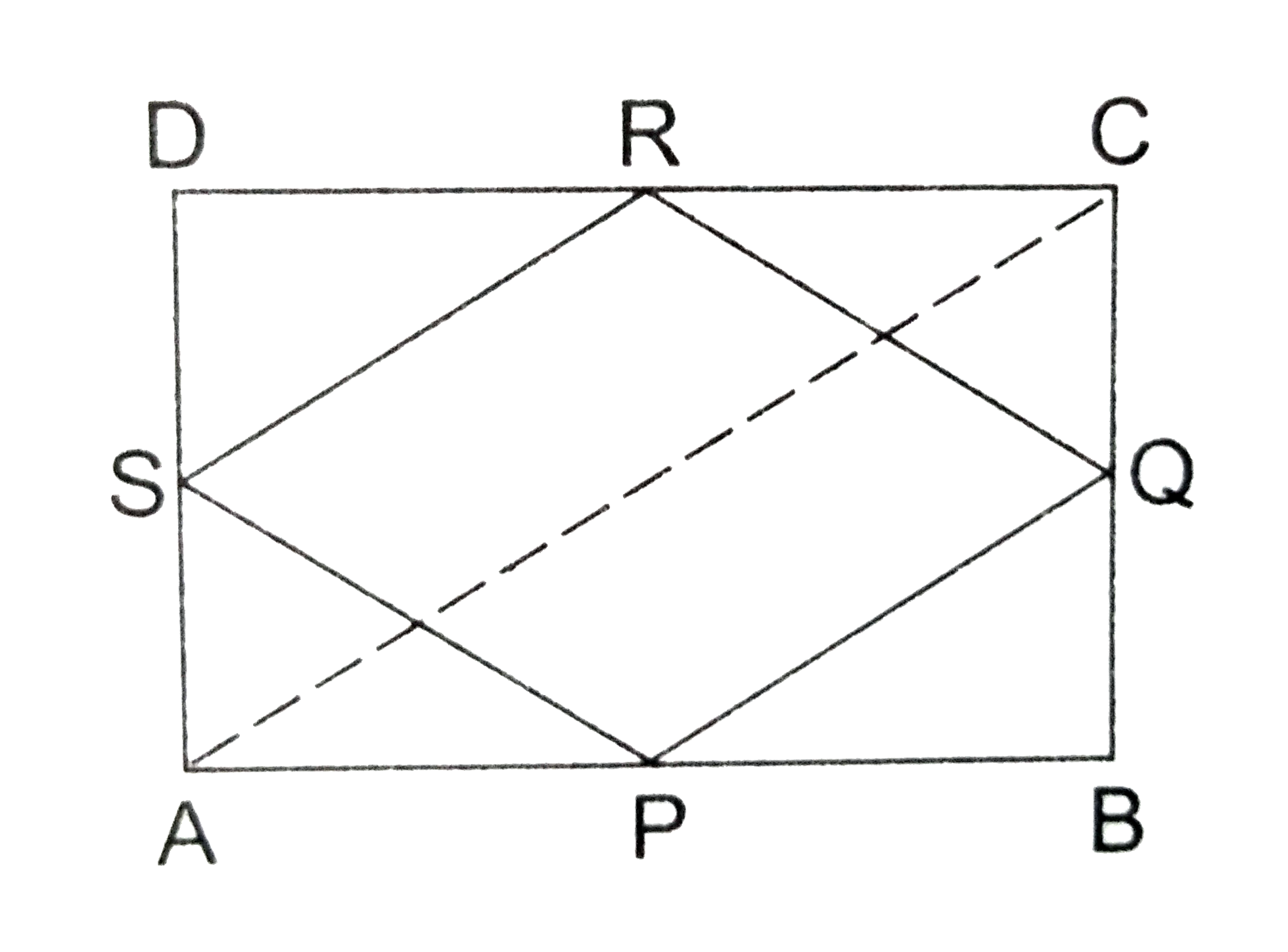
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
Let ABCD be a rectangle and P, Q, R S be the midpoints of AB, BC, CD and DA respectively. We have shown earlier the PQRS is a ||gm.
Now, △SAP≅△QBP
[∵AS=BQ,∠A=∠B=90∘andAP=BP].
∴PS=PQ.
Hence, PQRS is a rhombus.
Similar Questions
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionProve using vectors: The quadrilateral obtained by joining mid points of adjacent sides of a rectangle is a rhombus.
View Solution
