Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
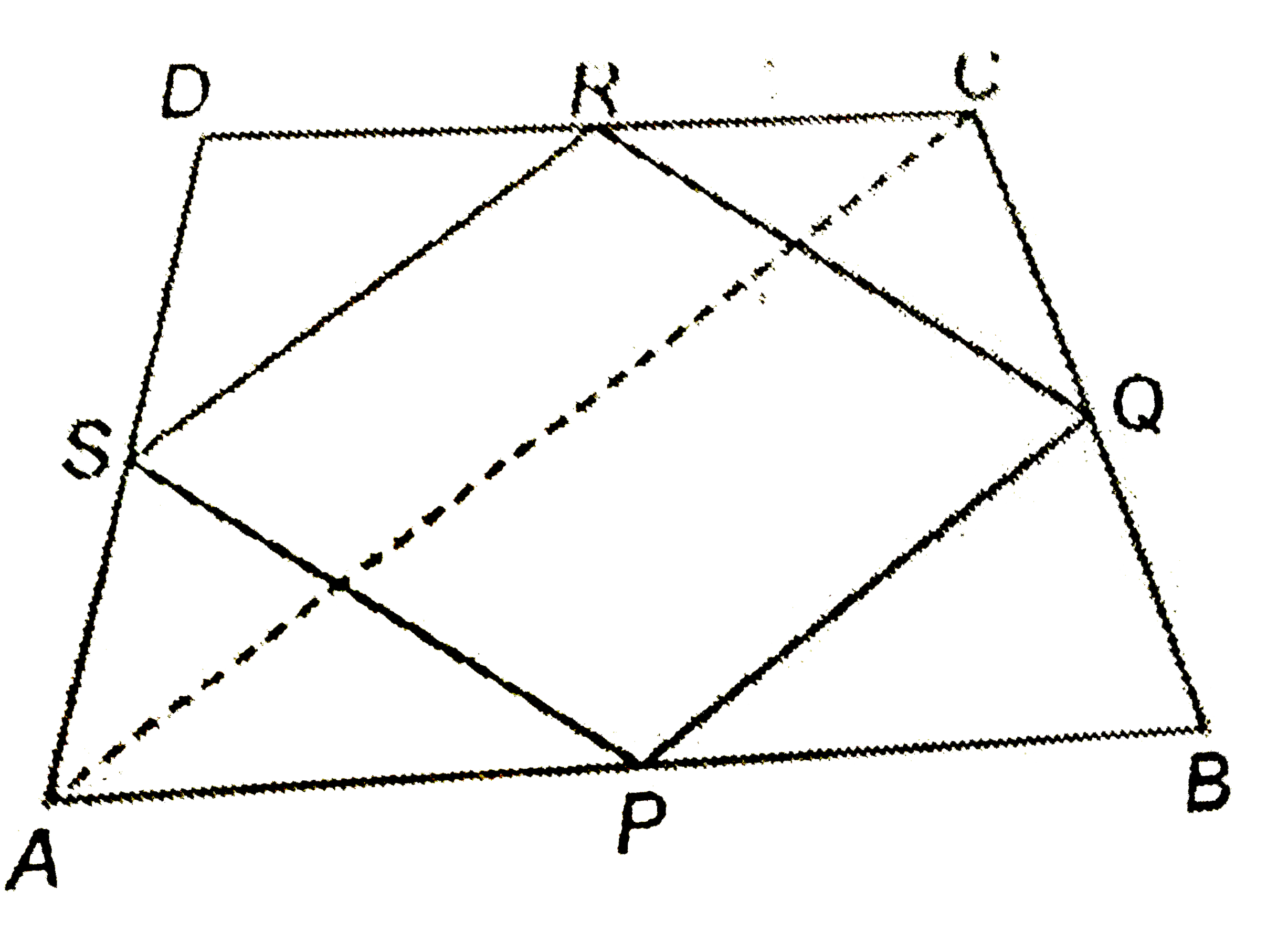
Given :□ABCD in which P,Q,R and S are respectively the mid-points AB, BC ,CD and DA.
To prove :□PQRS is a parallelogram.
Construction: Join AC.
Proof: In △ABC, since P and Q are the mid-points of AB and BC respectively.
∴PQ||ACandPQ=12AC (mid-point theorem)...(1)
Now, in △ADS, since S and R are the mid-point of AD and DC respectively.
∴SR∣∣ACandSR=12AC (mid-point theorem)...(2)
∴ From eqs. (1) and (2) , we get
PQ||SRandPQ=SR
Thus, in quadrilateral PQRS, one pair of opposite sides is parallel and equal.
Hence, □PQRS is a parallelogram. Hence proved.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Prove that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View Solution
Knowledge Check
The figure formed by joining the mid-points of adjacent sides of a rhombus is
Aa squareBrectangleCtrapeziumDnone of these
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle square (d) rhombus
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle (c) square (d) rhombus
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionProve that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View Solution

