Question

The diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.

Explanation

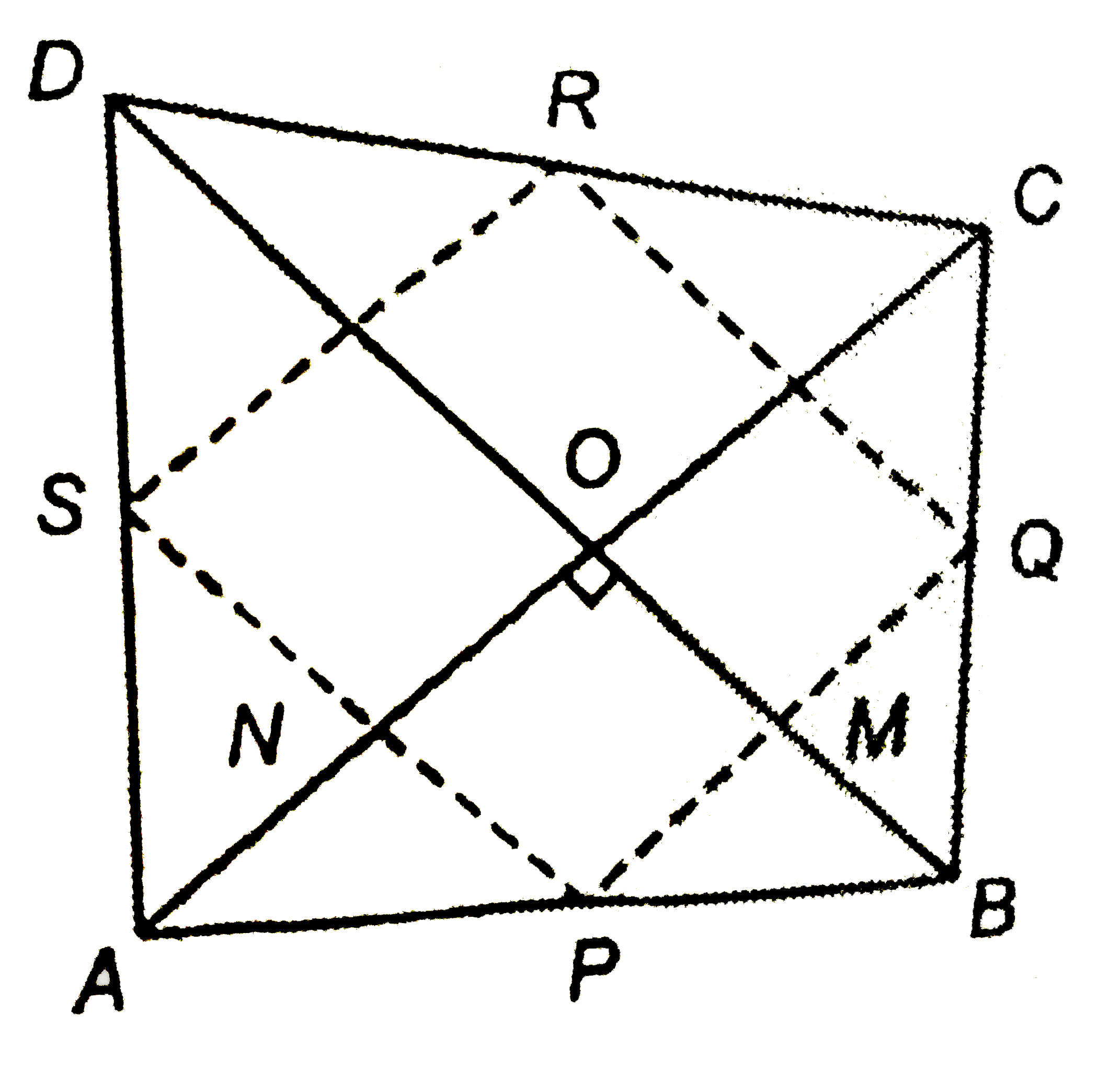
Let P, Q , R and S are the mid-points of the sides AB, BC,CD and DA respectively of `square ABCD`.
In `triangleBAC` , Since P is mid point of AB
and Q is mid-point of BC
`therefore PQ"||"AC and PQ=(1)/(2)AC` (mid-point theorem)…(1)
Similarly
`RS"||"AC and RS =(1)/(2)AC` (mid point theorem)...(2)
Form (1) and (2) , we get
`PQ"||"RS and PQ=RS`
`implies square PQRS` is a parallelogram. (`because` one pair of opposite sides is equal and parallel.)
Let the diagonals AC and BD of `square ABCD` intereset each other at point O.
In `triangleABD`, P is the mid point of AB and S is the mid-point of AD.
`therefore PS"||"BD`
`implies PN"||"MO`
Similarly, `PQ"||"AC`
`implies PM"||"NO`
`therefore sqaure PMON` is a parallelogram `" "` (pairs of opposite sides are parallel)
`implies angle MPN =angle MON`
`implies angle MPN=angleBOA`
`implies angleMPN=90^(@)" "(because angleBOA=90^(@), AC bot BD)`
`implies angleQPS=90^(@)`
Now, `squarePQRS` is a parallelogram and its one `angle is `90^(@)`
`therefore sqaure PQRS` is a rectangle. Hence proved.