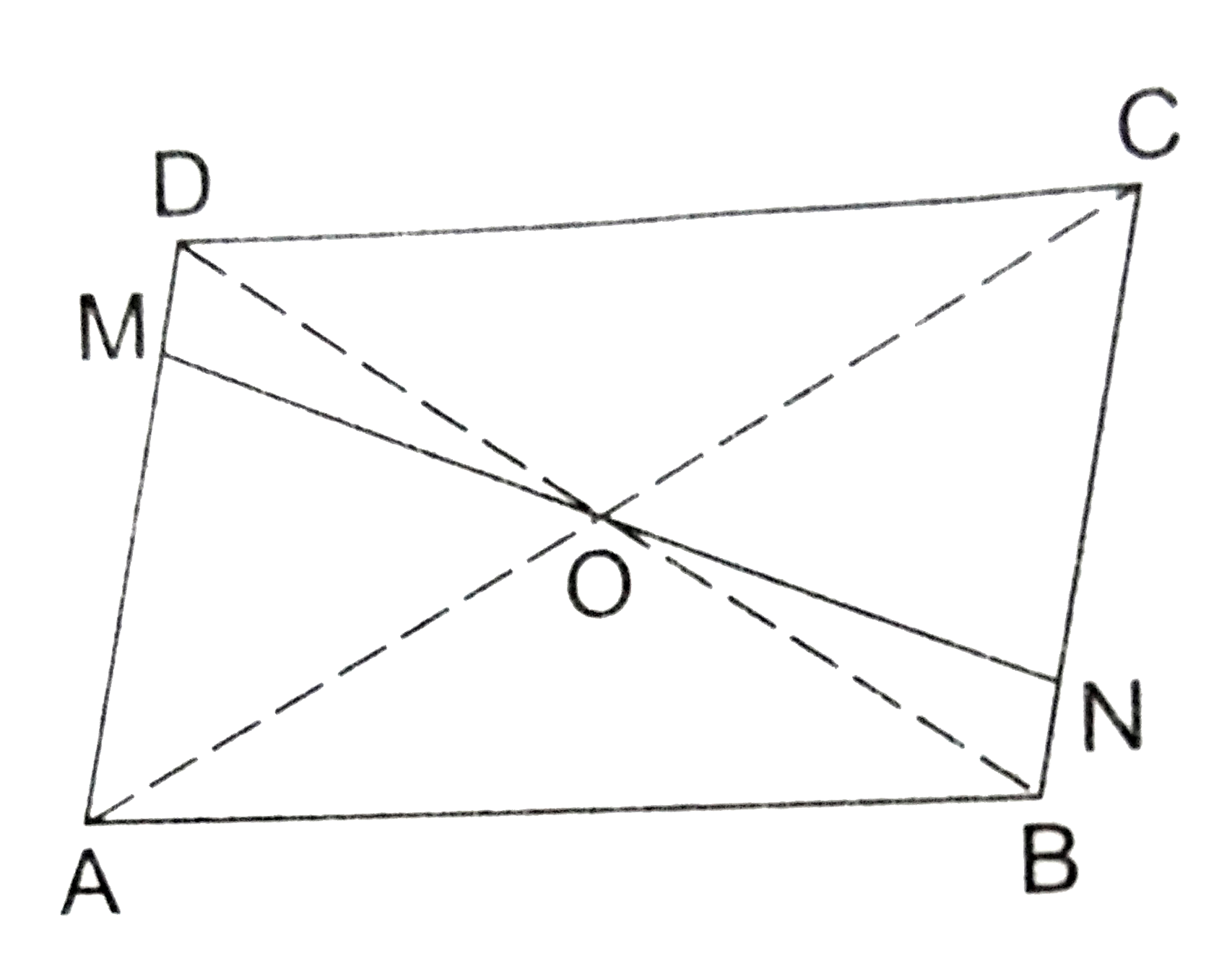
M and N are points on opposite sides AD and BC of a parallelogram ABCD such that MN passes through the point of intersection O of its diagoinals AC and BD. Show that MN is bisected at O.
△AOM≅△CON
[∵∠MAO=∠NCO,AO=CO,∠MOA=∠NOC]
[Note Diagonals of a ||gm bisect each other].
∴MO=NO (c.p.c.t.).
Similar Questions
P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
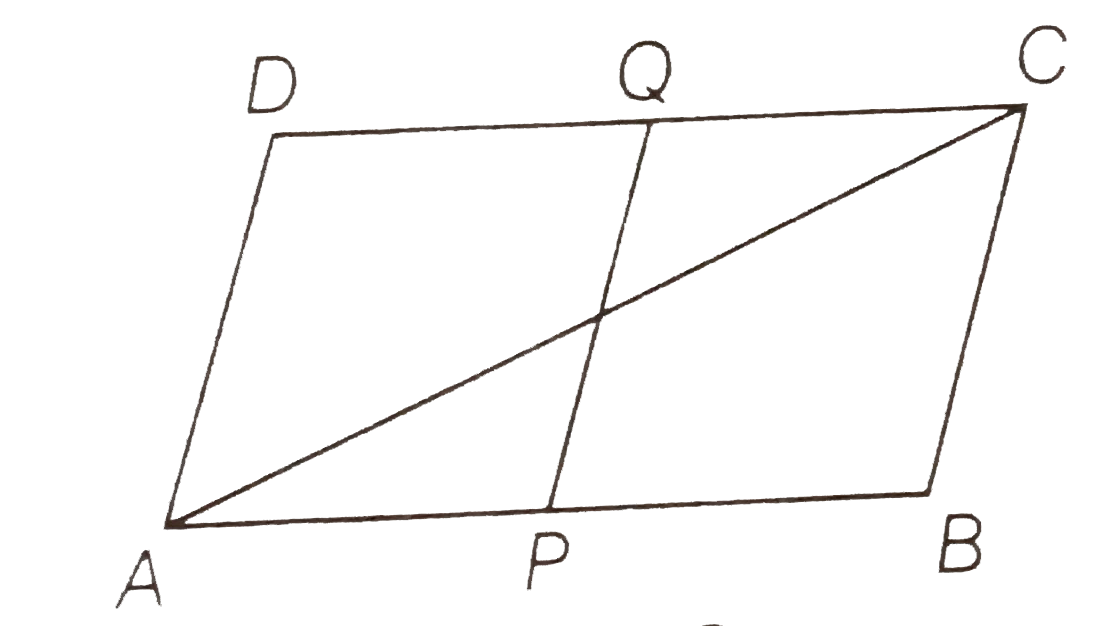
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
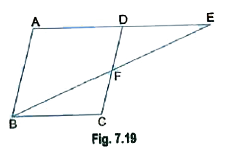
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.Show that ΔABE~ΔCFB.
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DFxEF=FBxFA.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View Solutiondiagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R. then
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the Side BC. Prove that DF×EF=FB×FA.
View Solution