In the given figure, equal chords AB and CD of a circle C(O,r) cut at right angles at E. If M and N are the midpoints of AB and CD respectively, prove that OMEN is a square.
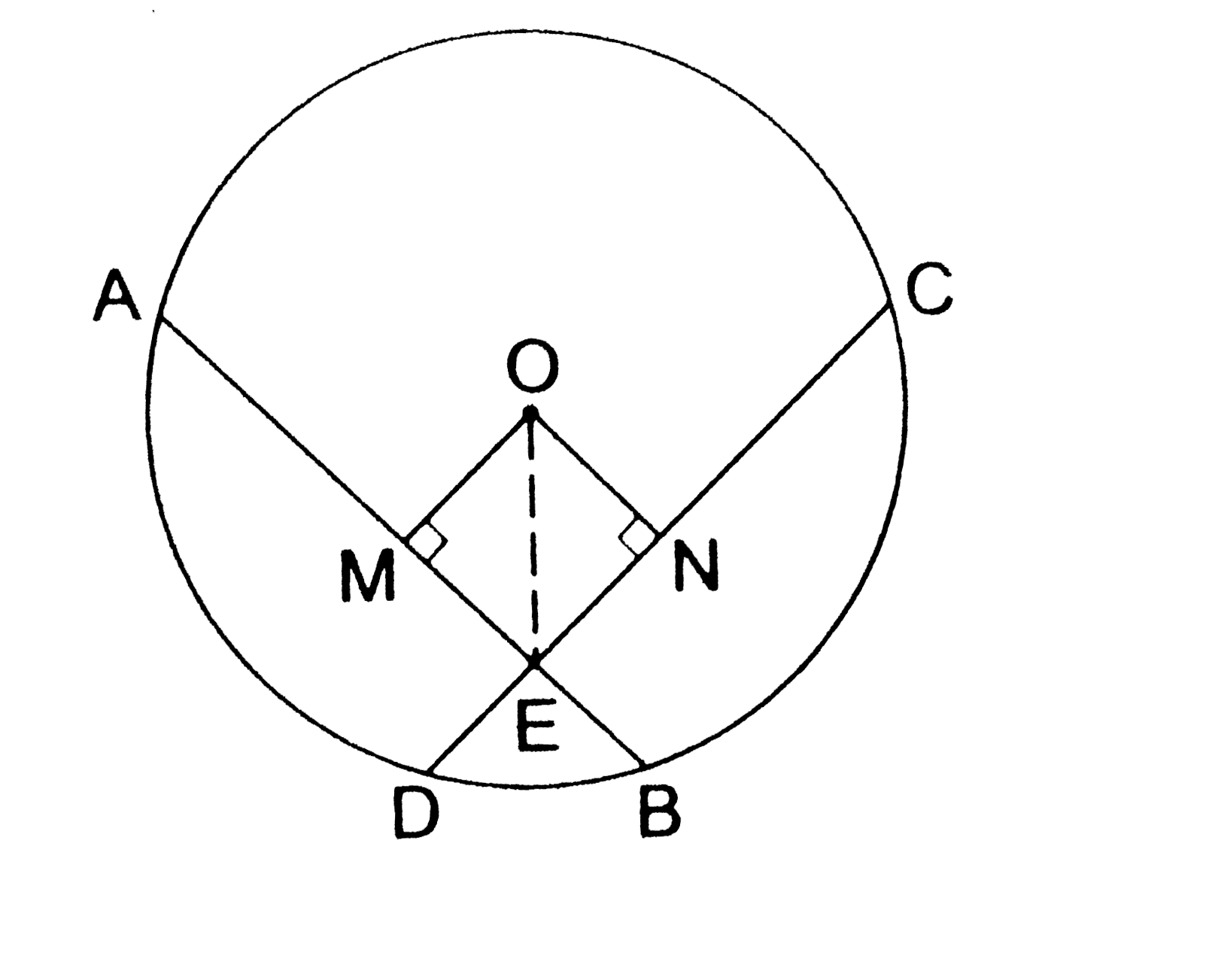
Given : A circle C(O,r) in which chord AB = chord CD, and N are the midpoints of AB and CD respectively.
To Prove : OMEN is a square.
Construction : Join OE
Proof : Since the line joining the centre of a circle to the midpoint of a chord is perpendicular to the chord, we have
OM⊥AG and ON⊥CD
⇒OMB=90∘ and ∠OND=90∘
⇒∠OME=90∘ and ∠ONE=90∘
Also, equal chords of a circle are equidistant from the centre.
∴OM=ON ....(i)
Now, in ΔOME and ΔONE, we have
OM = ON [ from (i) ]
∠OME=∠ONE [ each equal to 90∘]
OE=OE [ common]
∴ΔOME≅ΔONE[ by SAS -congruence ]
⇒ME=NE[ c.p.c.t. ]
Thus, in qud. OMEN, we have
OM=ON,ME=NE and ∠OME=ΔONE=90∘
Hence, OMEN is a square.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA65∘B55∘C70∘D50∘In the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
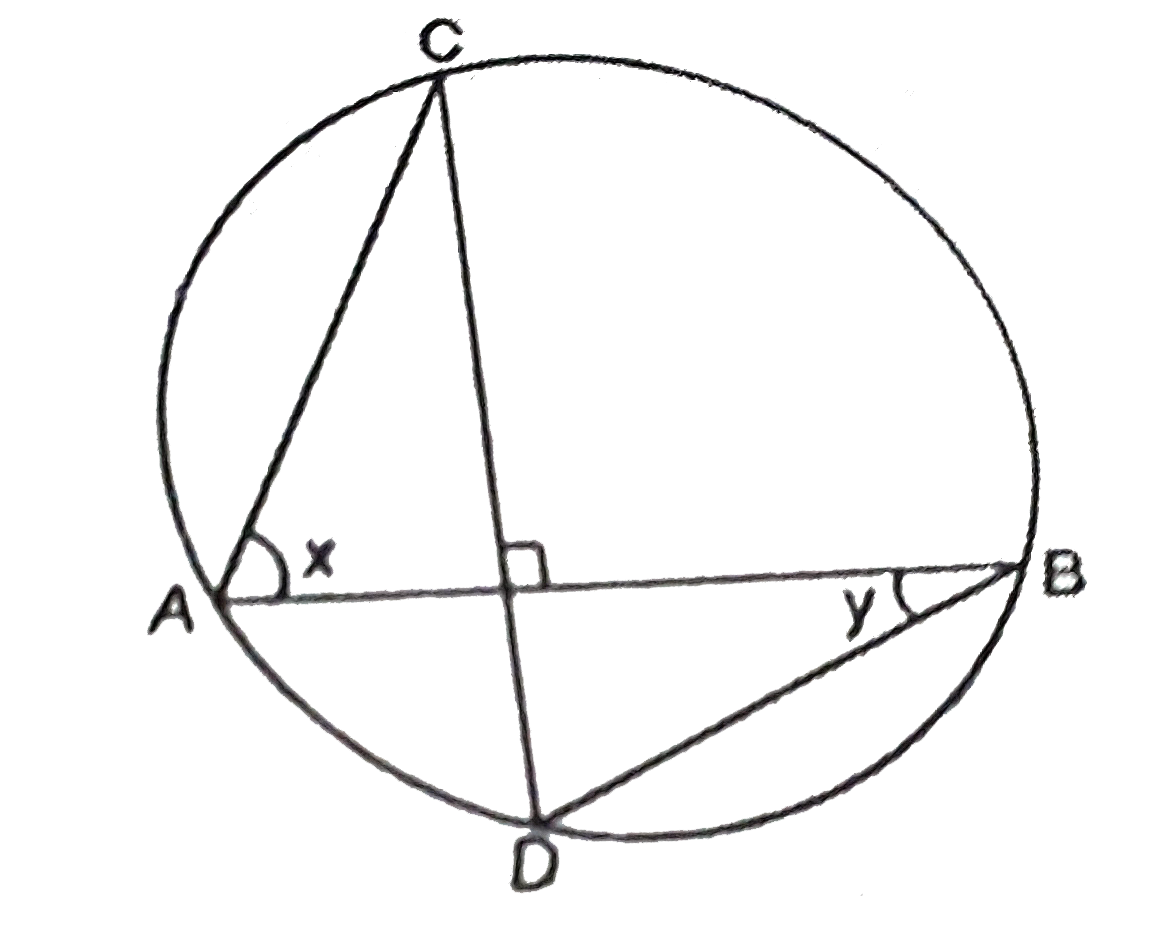 A45∘B90∘C120∘D100∘
A45∘B90∘C120∘D100∘
In the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
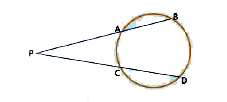
View SolutionIn the given figure,chords AB and CD of a circle intersect externally at P. AB=4 cm,CD=11 cm and PD=15 cm,then the length of PB is:
View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EP and FQ are the bisectors of ∠AEF and ∠EFD respectively, prove that EP∣∣FQ.

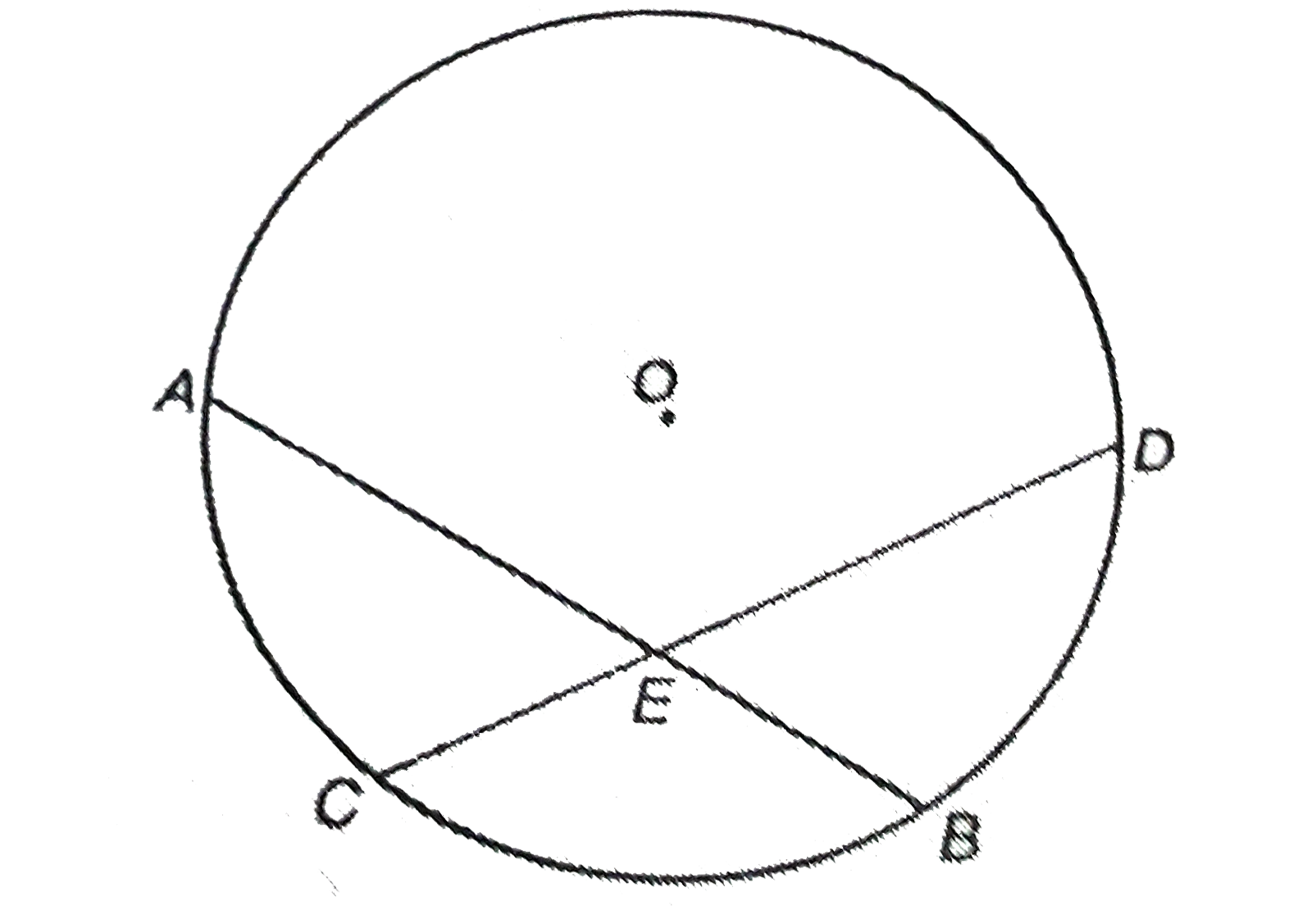
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EG and FG are this bisectors of ∠BEF and ∠EFD respectivelym prove that ∠EGF=90∘.

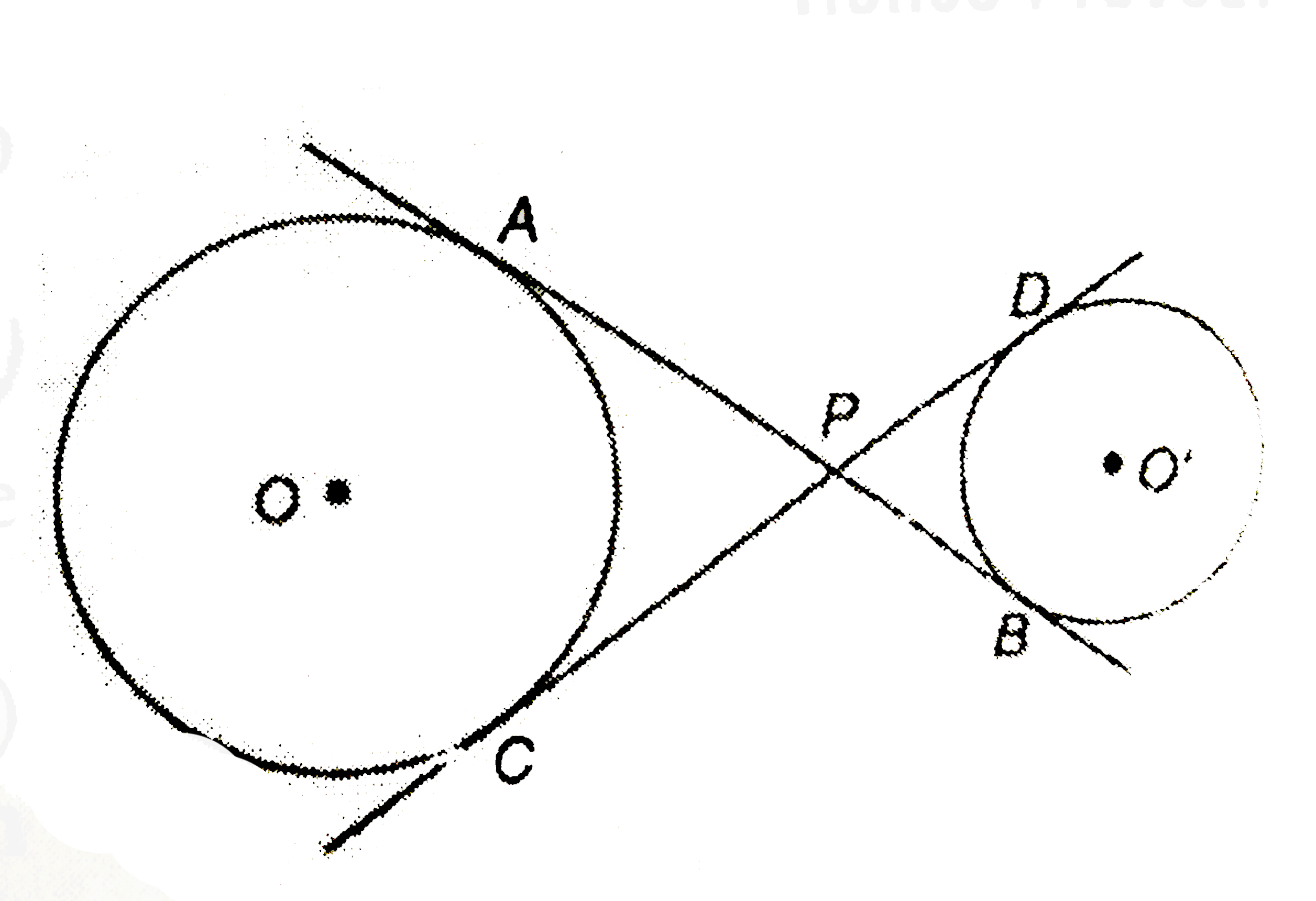
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
View Solution