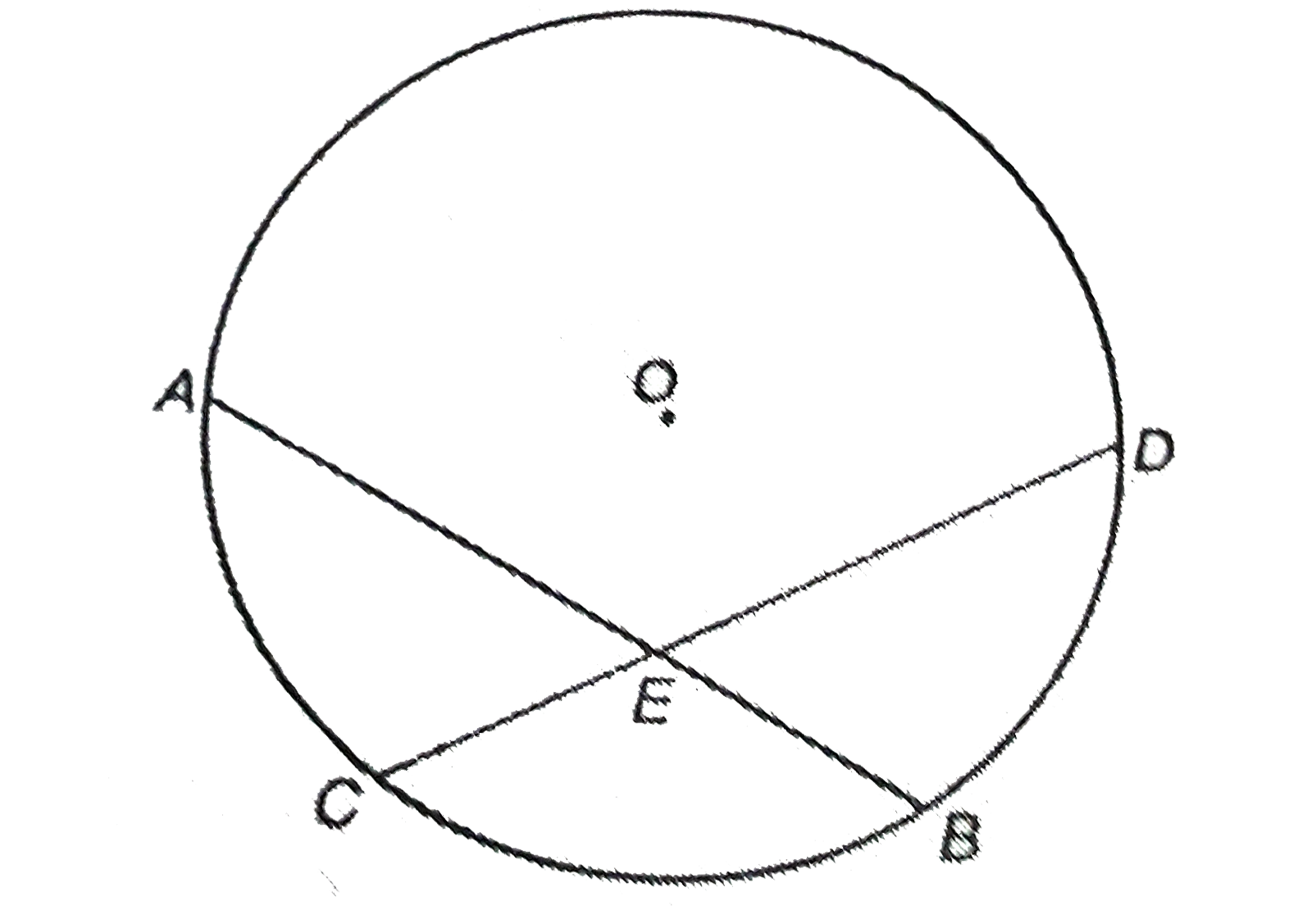
In the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
Video Solution
Text Solution
We have, ⇒
⌢AB≅⌢CD (if two chords of a circle are equal then their corresponding arcs are congruent)
Subtracting ⌢CB from both sides,we get
⌢AB−⌢CB≅⌢CD−⌢CB
⇒⌢AC≅⌢DB
⇒AC=DB (if two arcs are congruent then their corresponding chords are equal).
|
Similar Questions
Knowledge Check
In the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
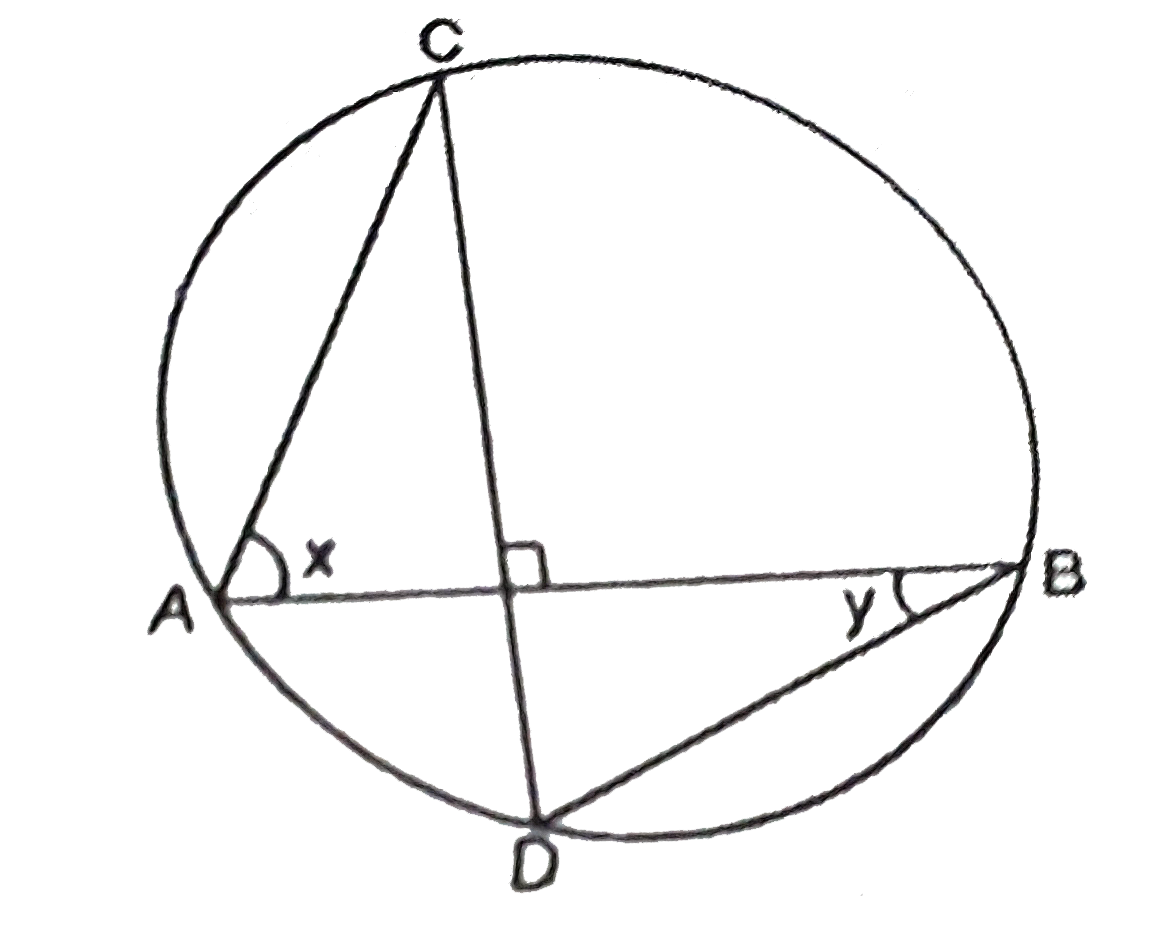 A45∘B90∘C120∘D100∘
A45∘B90∘C120∘D100∘Two chords AB and CD of a circle intersects each other at P. which of the following is correct?
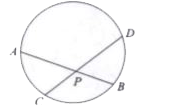 AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
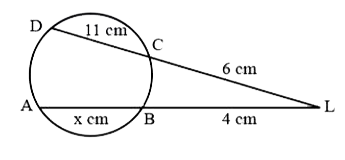
In the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
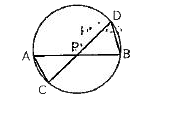
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
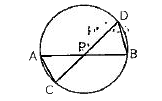
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
View SolutionIn the given figure, two chords AC and BD of a circle intersect at E.If arcAB=arcCD, prove that : BE=EC and AE=ED
View SolutionIn the adjoining figure chords AC and BD of a circle O, intersect at right angles at E. If ∠AOB=25∘ calculate ∠EBC
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD
View Solution