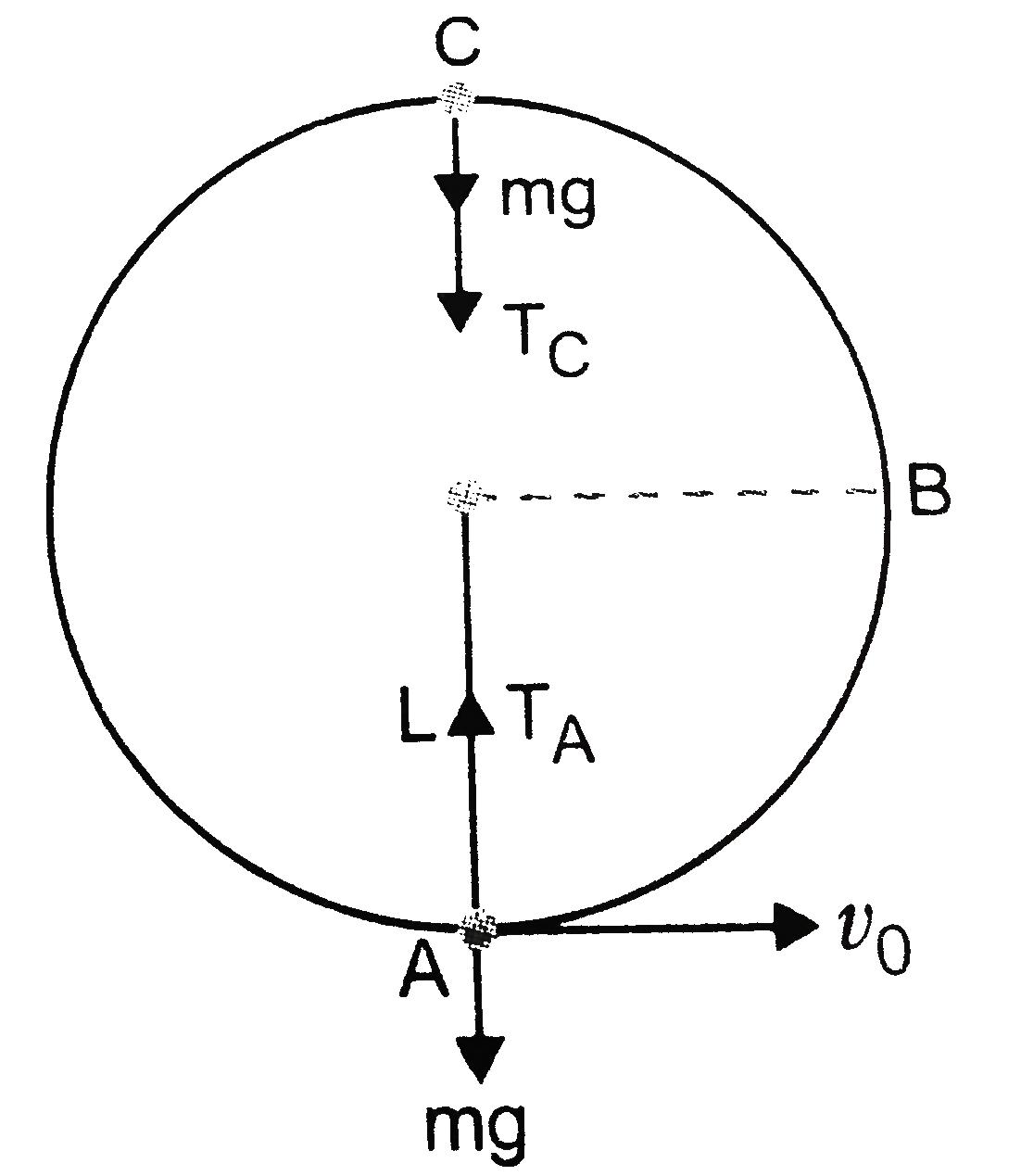
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 Solution in Tamil
Solution in Tamil
There are two external forces on the bob : gravity and the tension (T) in the string. The latter does no work since the displacement of the bob is always normal to the string. The potential energy of the bob is thus associated with the gravitational force only. The total mechanical energy E of the system is conserved. We take the potential energy of the system to be zero at the lowest point A. Thus, at A ,
E=12mv20 (6.12)
TA−mg=mv20L [Newton.s Second Law]
where TA is the tension in the string at A. At the highest point C, the string slackens, as the tension in the string (TC) becomes zero.
Thus, at C E=12mv2c+2mgL (6.13)
mg=mv2cL [Newton.s Second Law] (6.14)
where vc is the speed at C. From Eqs. (6.13) and (6.14)
E=52mgL
Equatting this to the energy at A 52mgL=m2v20
or, v0=√5gL.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES
46 Videos
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES (ADDITIONAL EXERCISES)
7 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
Similar Questions
The sign of work done by a force is important to understant. State carefully if the following quantities are positive or negative. (a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket. (b) Work done by the gravitational force in the above case. (c ) Work done by friction on a body sliding down an inclined plane. (d) Work done by an applied froce on a body moving on a rough horizontal plane with uniform velocity. (e ) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionThe speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.

View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at (a) Point B ? (b) Point C? (c) Point X?
View Solutionm द्रव्यमान का एक गोलक L लंबाई की हल्की दूरी से लटका हुआ है । इसके निम्नतम बिंदु A पर क्षैतिज वेग v0 इस प्रकार लगाया जाता है कि यह ऊर्ध्वाधर तल में अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है कि दूरी केवल उच्चतम बिंदु C पर ढीली होती है , जैसा कि चित्र में दर्शाया गया है । निम्न राशियों के लिए व्यंजक प्राप्त कीजिए -
( a ) v0
( b ) बिंदुओं B तथा C पर गोलक की चाल तथा
( c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KBKC)
गोलक के बिंदु C पर पहुँचने के बाद पथ की आकृति पर टिपण्णी कीजिये ।
View Solutionm द्रव्यमान का एक गोलक L लम्बाई की हल्की डोरी से लटका हुआ है। इसके निम्नतम बिंदु A पर क्षैतिज वेग v0 इस प्रकार लगाया जाता है की यह ऊर्ध्वाधर तल से अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है की डोरी केवल उच्चतम बिंदु C पर ढीली होती है जैसा की चित्र में दिखाया गया है। निम्न राशियों के लिये व्यंजक प्राप्त कीजिये - (a ) v0 (b ) बिन्दुओ B तथा C पर गोलक की चाल तथा (c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KBKC) गोलक के बिंदुC पर पहुँचने के बाद पथ की प्रकृति पर टिप्पणी कीजिये।
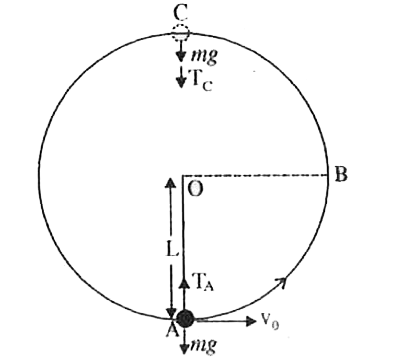
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
vo
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The speeds at points B and C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The ratio of the kinetic energies (KB/KC) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
vo
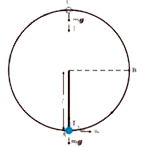
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The speeds at points B and C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. Obtain an expression for
The ratio of the kinetic energies (KB/KC) at B and C.
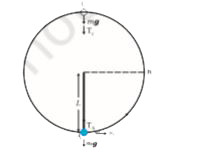
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for v_(o)
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The speeds at points B and C.
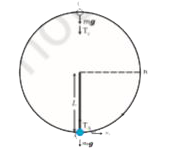
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The ratio of the kinetic energies (K_(B)"/"K_(C )) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
View Solution
