In the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.

Video Solution

Text Solution

Verified by Experts

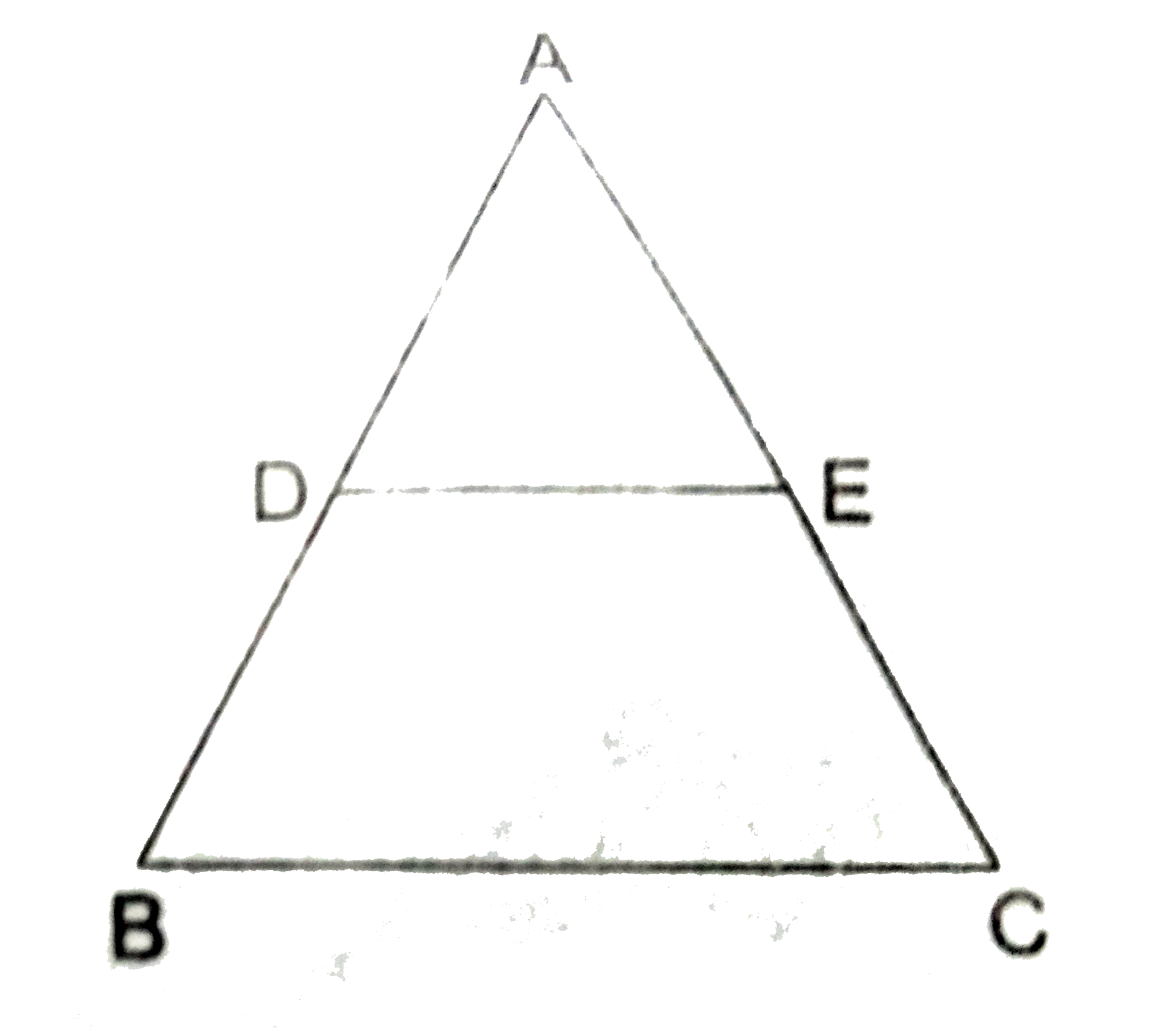
$A B = B C and A D = A E$
$\Rightarrow A B - A D = A C - A E \Rightarrow D B = E C$
$\Rightarrow \frac{A D}{A E} = \frac{D B}{E C}$ [ each equal to 1]
$\Rightarrow D E ∣ ∣ B C$ [ by the converse of Thale's theorem]
$\Rightarrow ∠ D E C + ∠ E C B = 180^{\circ}$
$\Rightarrow ∠ D E C + ∠ C B D = 180^{\circ} = [∴ A B = A C \Rightarrow ∠ C = ∠ B]$
$\Rightarrow$ quad. BCED is cyclic.

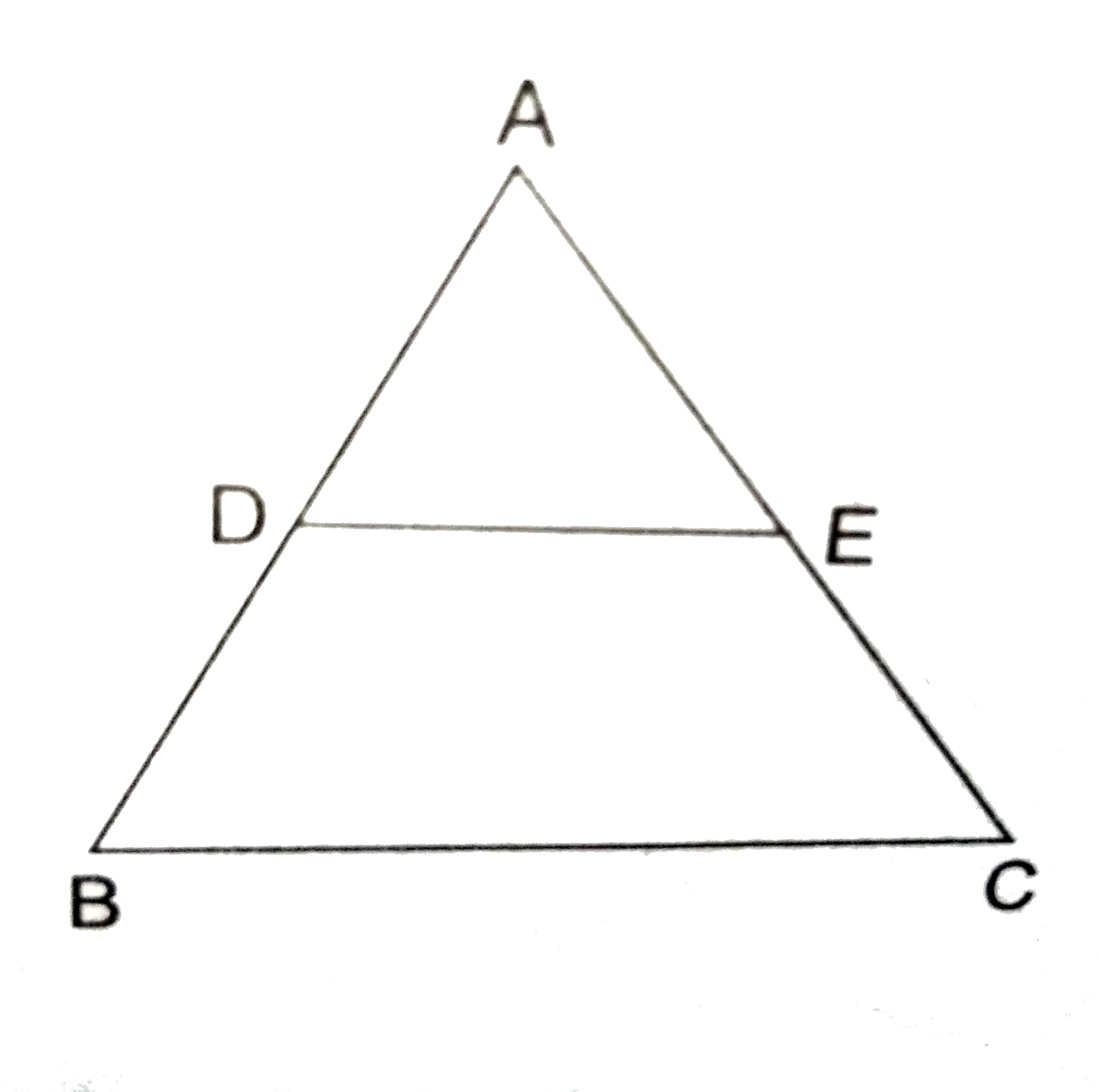
Hence, the points, B,C,E ,D are concylic.

Updated on:21/07/2023

In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then

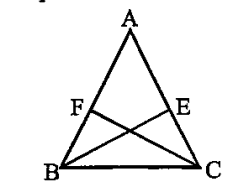ABE=CF
B $∠ B F C = ∠ C E B$
CBF=CE
DAll of these
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then

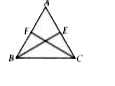ABE = CF
B $∠ B F C = ∠ C E B$
CBF = CE
DAll of these
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
A $\frac{a}{4} - \frac{b}{4}$
B $\frac{a}{2} - \frac{b}{2}$
C $\frac{b}{4} - \frac{a}{4}$
D $\frac{b}{2} - \frac{a}{2}$