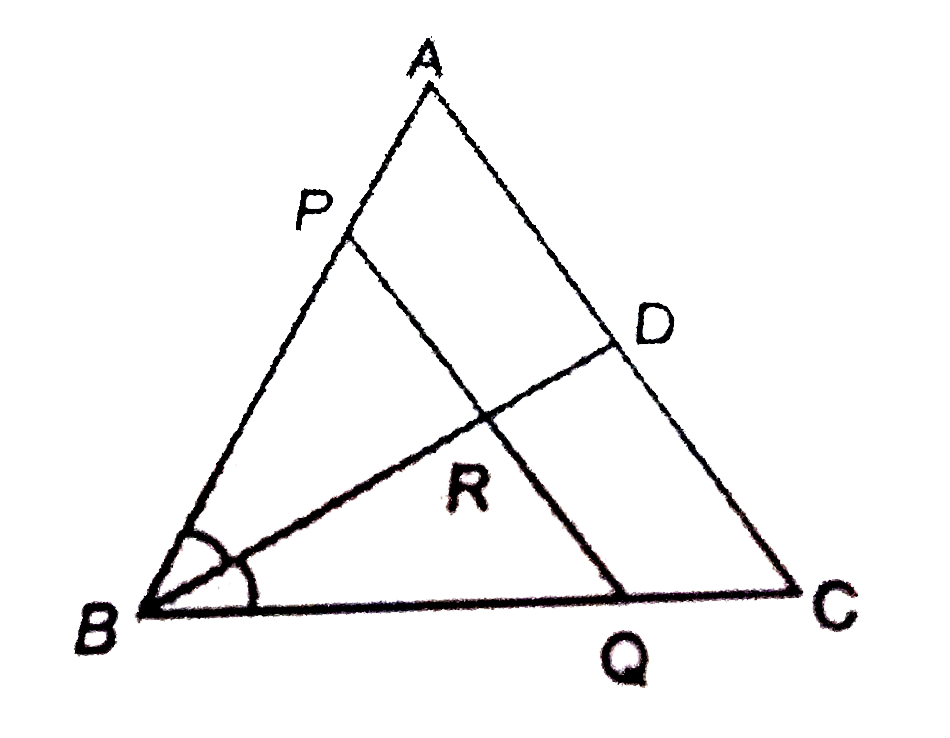
In $Δ A B C$ , the bisector of $∠ B$ meets AC at D. A line $P Q ∣ ∣ A C$ meets AB,BC and BD at P,Q and R respectively. Show that $B P \times Q R = B Q \times P R$ .

Video Solution

Text Solution

Verified by Experts

In $Δ B Q P, B R$ is the bisector of $∠ B$ .
$∴ \frac{Q R}{P R} = \frac{B Q}{B P}$ [ by angle-bisector theorem]

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7B
19videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C
13videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27videos
T-RATIOS OF SOME PARTICULAR ANGLES
BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20videos
TRIGONOMETRIC IDENTITIES

Similar Questions

Knowledge Check

Question 1 - Select One or More
In $Δ A B C$ , internal angle bisector of $∠ A$ meet side BC in D. $D E ⊥ A D$ meet AC in E and AB in F. then
AAE in H.M of b and c
B $A D = \frac{2 b c}{b + c} cos . \frac{A}{2}$
C $E F = \frac{4 b c}{b + c} sin . \frac{A}{2}$
D $Δ A E F$ is isosceles
Question 2 - Select One
ABC is a cyclic triangle and the bisectors of $∠ B A C, ∠ A B C and ∠ B C A$ meet the circle at P,Q and R respectively. Then the angle $∠ R Q P$ is:
A $90^{\circ} - \frac{∠ B}{2}$
B $90^{\circ} + \frac{∠ B}{2}$
C $90^{\circ} + \frac{∠ C}{2}$
D $90^{\circ} + \frac{∠ B}{2}$
Question 3 - Select One
In a $Δ A B C, ∠ C$ in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and E respectively . If $A B = A D = B E$ . Find $∠ A C B$ .
A $105^{\circ}$
B $108^{\circ}$
C $110^{\circ}$
D $135^{\circ}$

RS AGGARWAL-TRIANGLES-Exercise 7A

Home
Ask Doubt
Profile