ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ . If PQ produced meets BC at R, prove that R is the midpoint of BC.
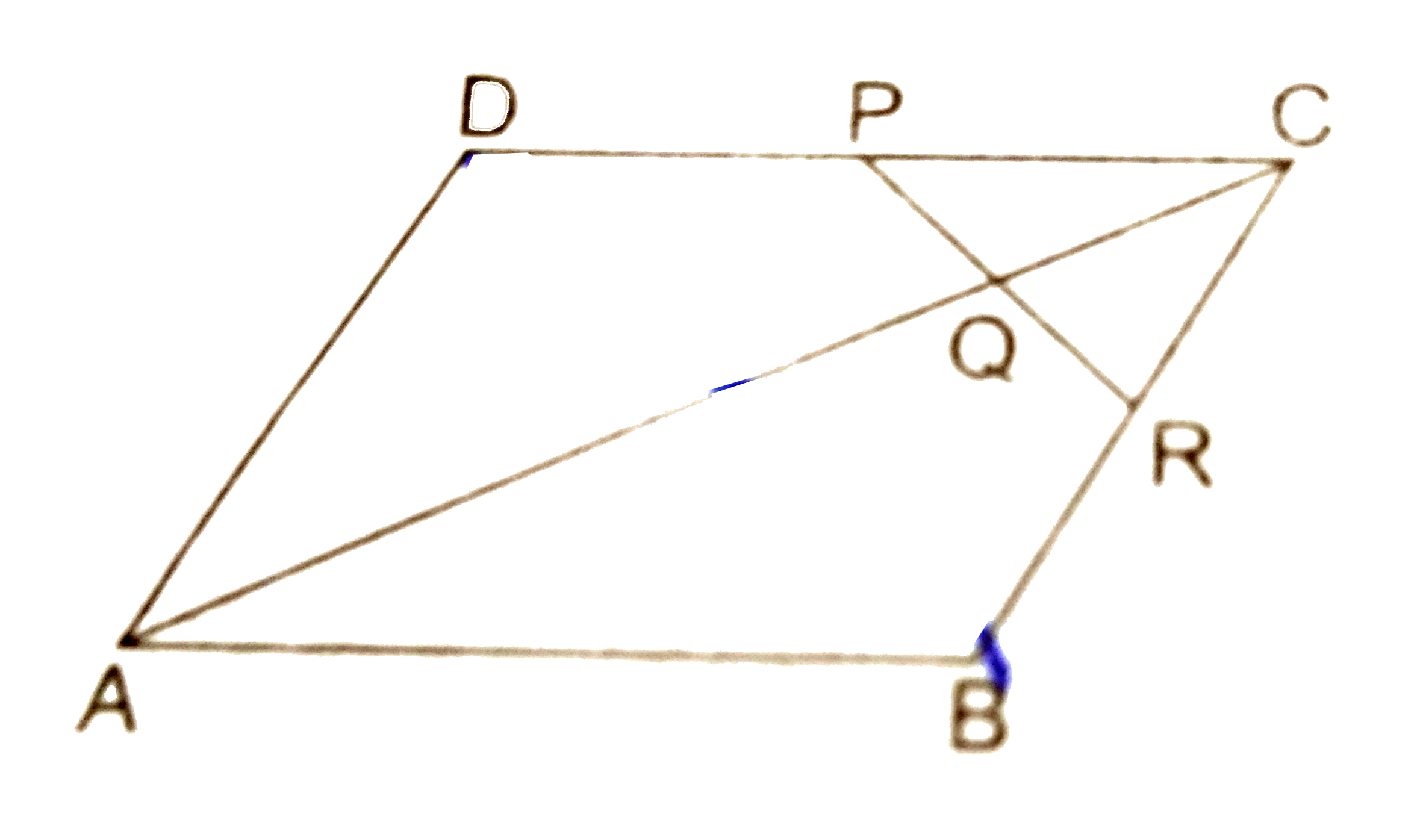
Join BD. Suppose it meets AC at S.
Since the diagonals of ||gm bisect each other, .
Now,.
is the midpoint of CS.
So, and therefore .
In is the midpoint of Cs and , so R is the midpoint of BC.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7B
Explore 19 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7C
Explore 13 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
ArectangleBsquareCparallelogramDrhombusABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD)
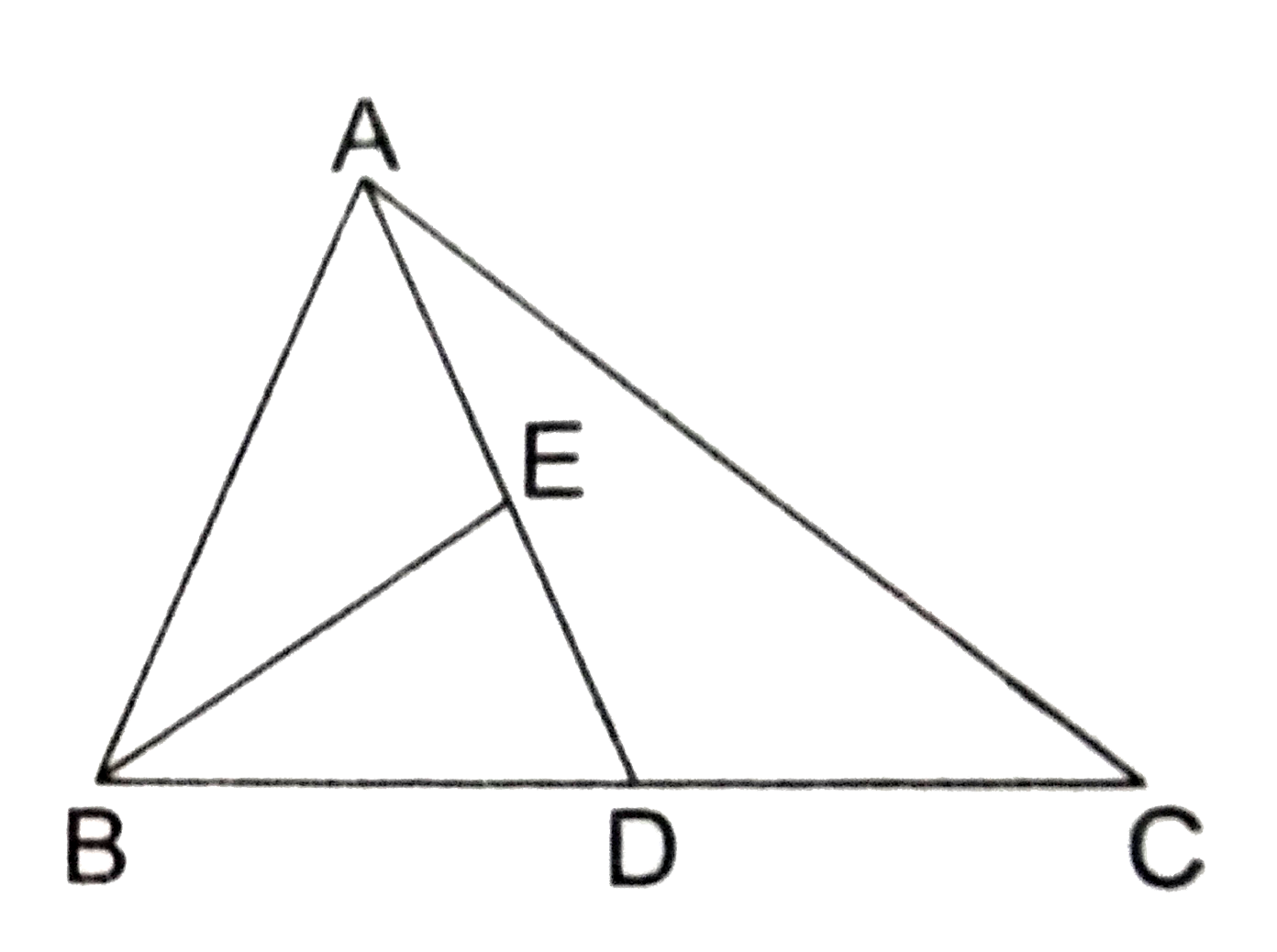
In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
View SolutionABCD is a parallelogram. Any line through A cuts DC at a point P and BC produced at Q.Then,
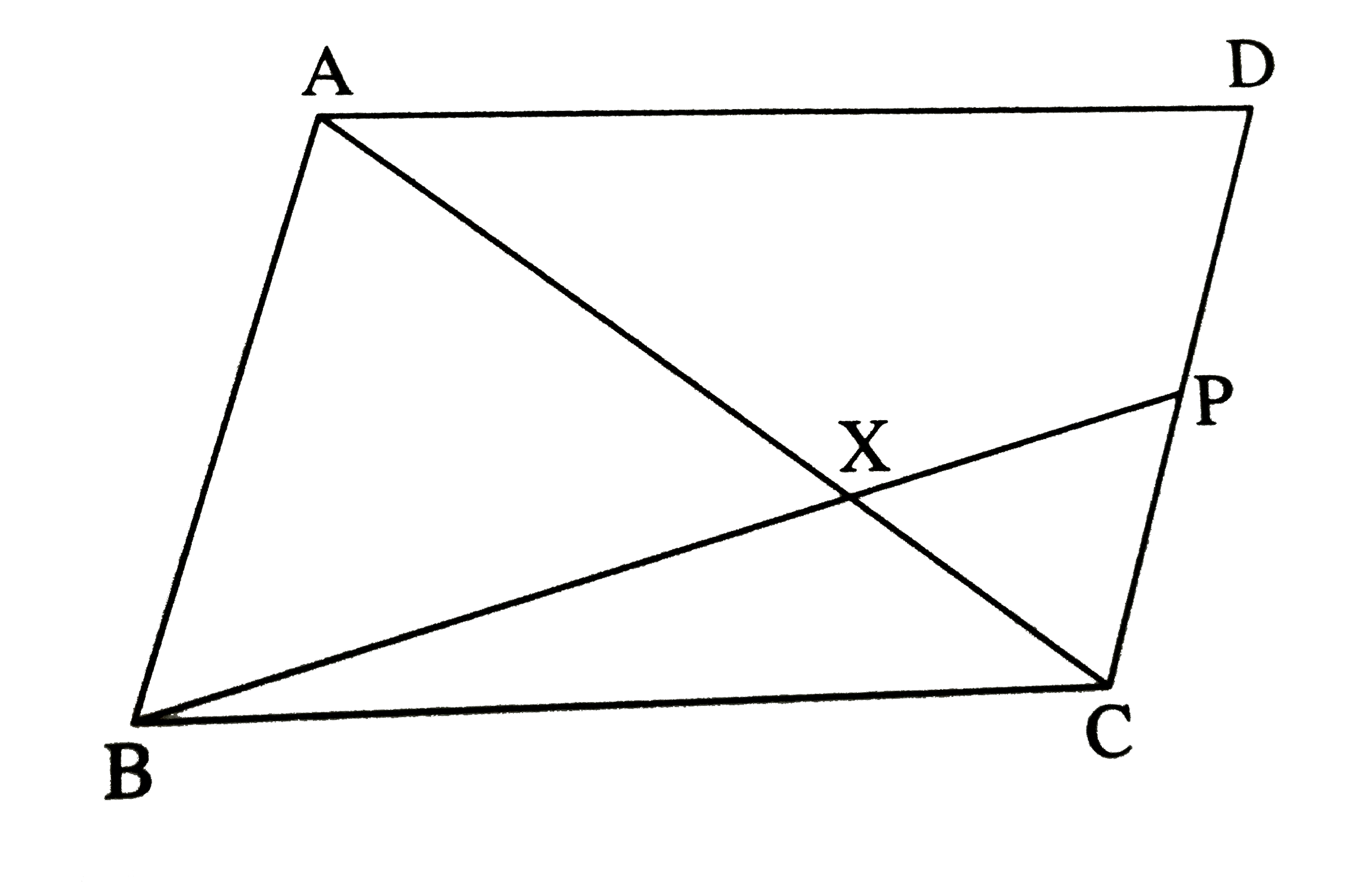
View Solution□ABCD is a parallelogram. P is the midpoint of side CD. Seg BP meets diagonal AC at X. Prove that 3AX=2AC.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution

