ΔABCandΔDBC lie on the same side of BC, show in the figure. From a point on BC.PQ||ABandPR||BD are drawn, meeting AC at Q, and CD at R respectively. Prove that QR∣∣AD.
In ΔCAB,QP∣∣AB⇒CPPB=CQQA
In ΔCDB,RP∣∣DB⇒CPPB=CRRD
∴CQQA=CRRD⇒QR∣∣AD(inΔCDA)
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7B
19 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
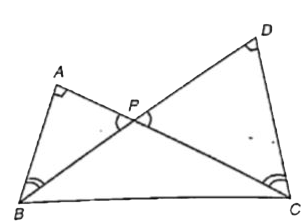 AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
ΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
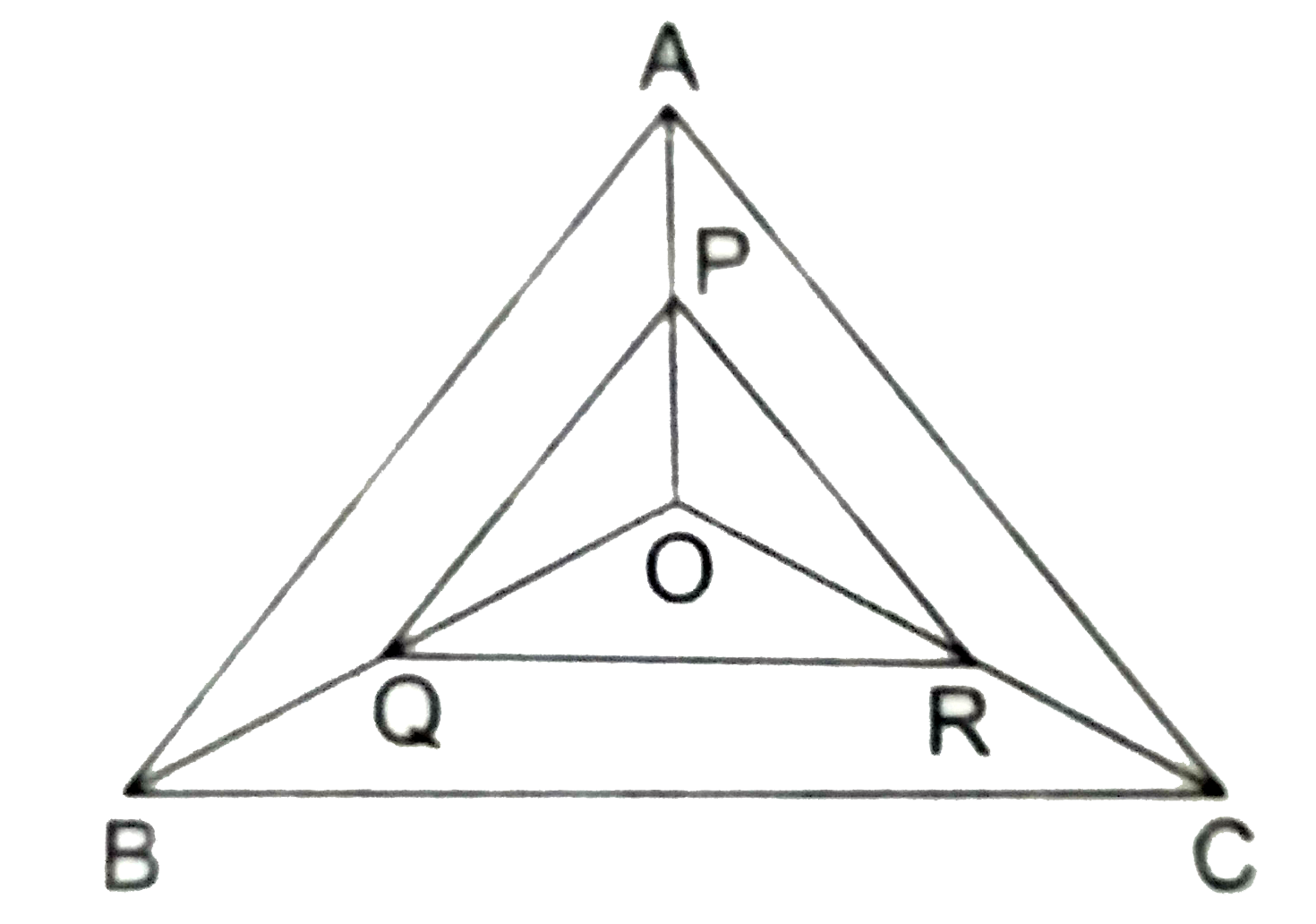
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionIn ΔABC, the bisector of ∠B meets AC at D. A line PQ∣∣AC meets AB,BC and BD at P,Q and R respectively. Show that BP×QR=BQ×PR.
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
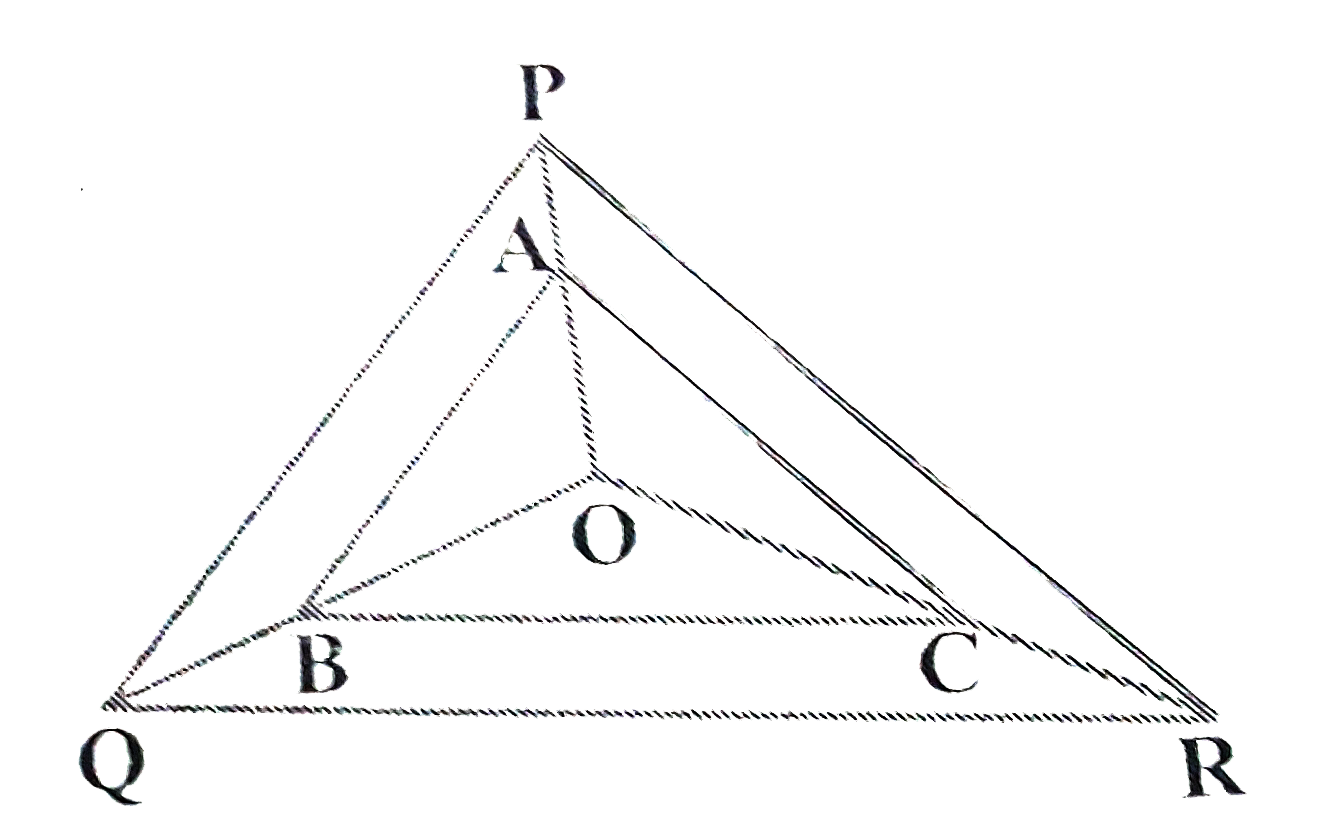
View Solution
