In the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
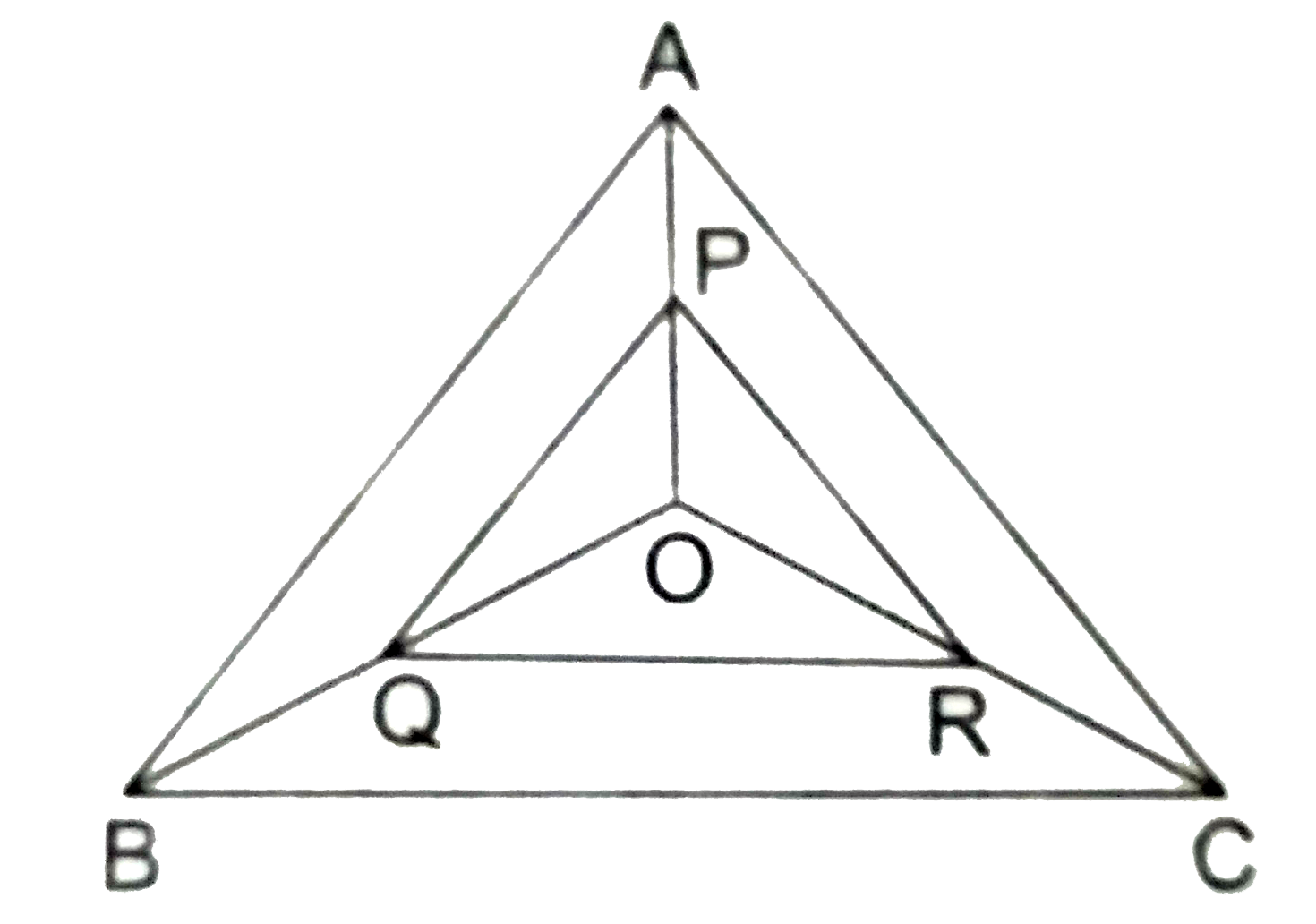
In ΔOAB,PQ∣∣AB.
∴OPPA=OQQB ..(i) [ by Thale's theorem]
In ΔAOC,PR∣∣AC.
∴OPPA=ORRC ....(ii) [ by Thale's theorem]
From (i) and (ii), we get
OQQB=ORRCinΔOBC.
Thus, in ΔOBC,QandR and points in OB and OC respectively such taht OQQB=ORRC
Hene, by the converse Thale's theorem, QR∣∣BC
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
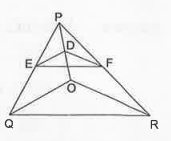
In the figue given along side, DE||OQandDF||OR. Show that EF∣∣QR.
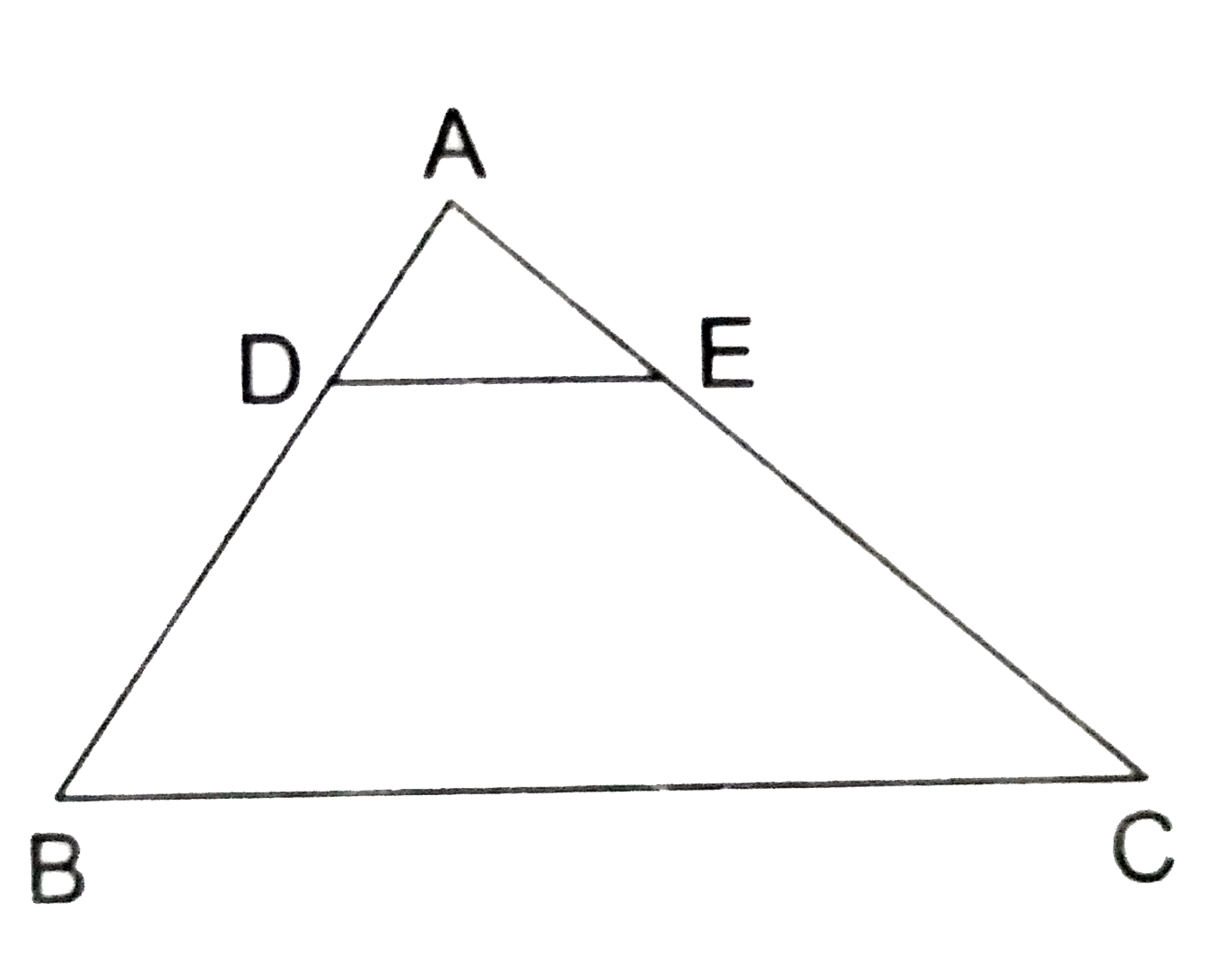
View SolutionD and E are points on the sides AB and AC respectively of a ΔABC such that DE∣∣BC.
(i) If AD=3.6cm,AB=10cmandAE=4.5cm, find EC and AC.
(ii) If AB=13.3cm,ac=11.cm,andEC=5.1cm, find AD
(iii) If ADDB=47andAC=6.6cm, find AE.
(iv) If ADAB=815andEC=3.cm, find AE.
View SolutionFind the value of sin60∘cos30∘+cos60∘sin30∘.
View Solutioncos256∘+cos234∘sin∘56∘+sin234∘+3tan256∘tan234∘=?
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of figure given below.
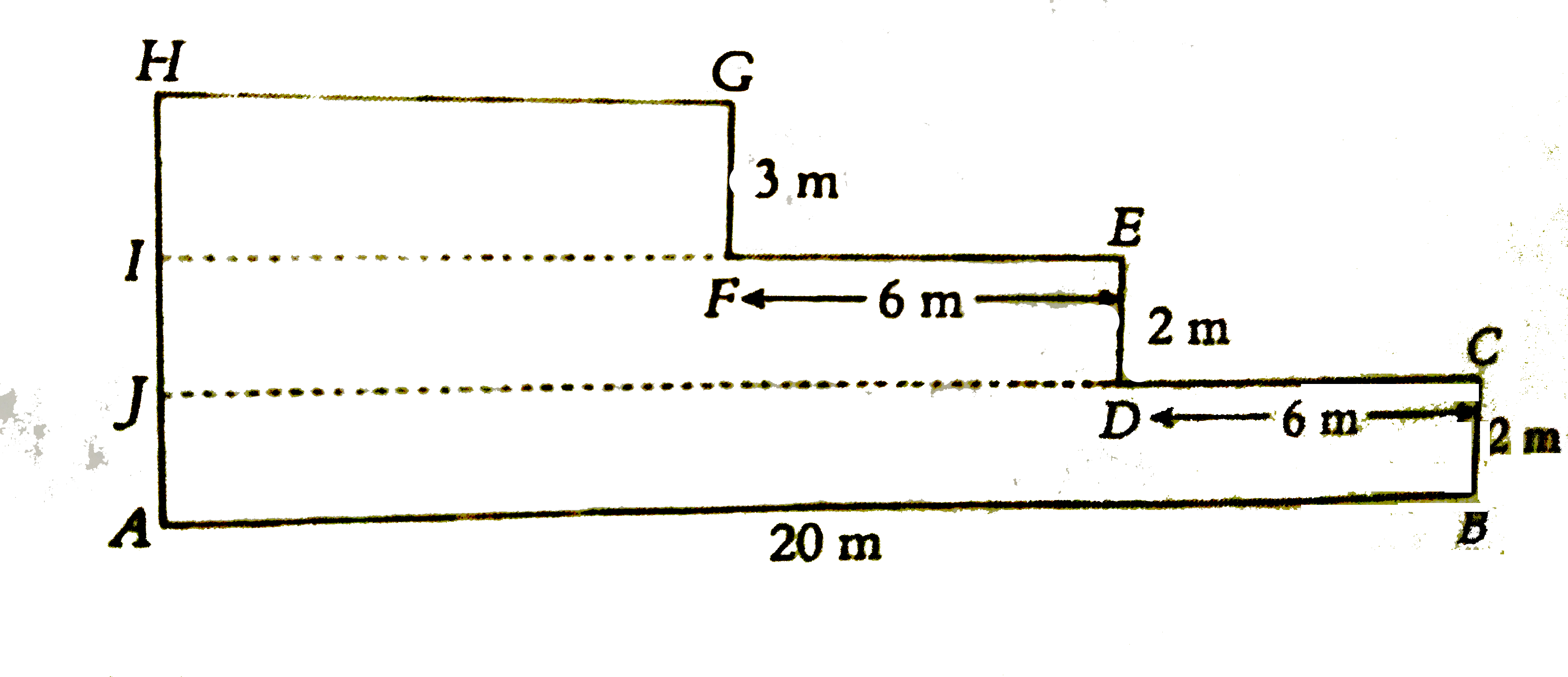
View SolutionFind the perimeter of the figure given below.
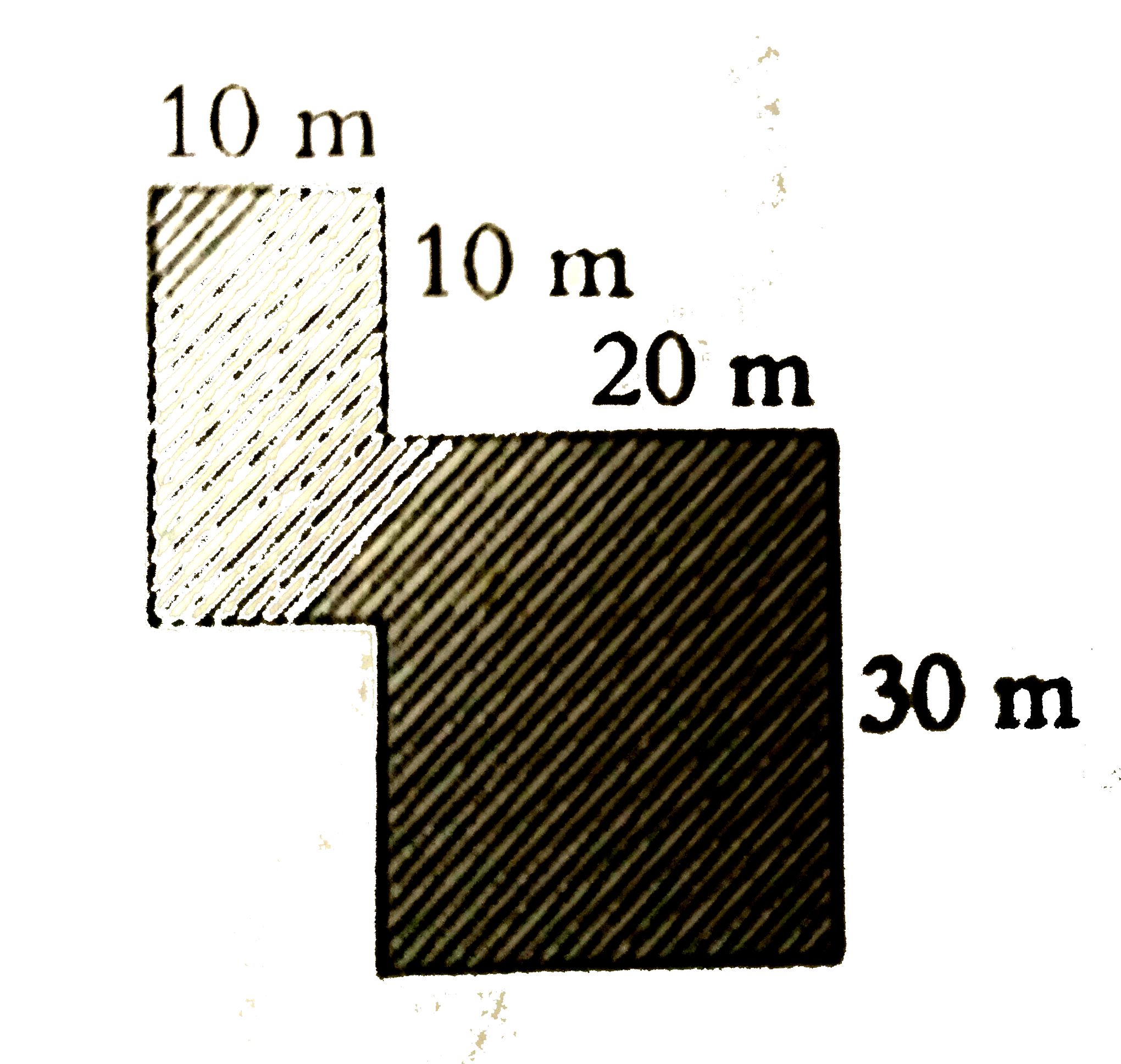
View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View Solution

