ABCD is a parallelogram. Any line through A cuts DC at a point P and BC produced at Q.Then,
Area(△BPC)=Area(△DPQ)
Area(△BPC)=14Area(△ACB)
Area(△DPQ)=14Area(△ADP)
None of these
To solve the problem involving the parallelogram ABCD and the points P and Q, we will proceed step by step.
1. Draw the Parallelogram:
- Begin by sketching the parallelogram ABCD with vertices A, B, C, and D. Ensure that opposite sides are parallel and equal in length.
Hint: Remember that in a parallelogram, opposite sides are equal and parallel.
2. Identify Points P and Q:
- Draw a line through point A that intersects line DC at point P and extends to intersect the line BC (produced) at point Q.
Hint: Visualize the intersections clearly; P is on line DC, and Q is on the extended line BC.
3. Triangles Involved:
- Identify the triangles formed: Triangle ACP and Triangle BCP. Notice that both triangles share the base CP.
Hint: When comparing areas of triangles, look for shared bases and heights.
4. Area of Triangle ACP:
- The area of triangle ACP can be expressed as:
Area of △ACP=12×AC×h1
where h1 is the height from point P to line AC.
Hint: The area of a triangle can be calculated using the formula 12×base×height.
5. Area of Triangle BCP:
- Similarly, the area of triangle BCP can be expressed as:
Area of △BCP=12×BC×h2
where h2 is the height from point P to line BC.
Hint: Since ABCD is a parallelogram, AC is parallel to BC, which helps in establishing relationships between the triangles.
6. Equating Areas:
- Since triangles ACP and BCP share the same height from point P to line AC and BC, we can conclude:
Area of △ACP=Area of △BCP
Hint: Use the property of triangles sharing a common height to equate their areas.
7. Area of Triangle ADQ:
- Now consider triangle ADQ. The area can be expressed as:
Area of △ADQ=12×AD×h3
where h3 is the height from point Q to line AD.
Hint: Remember that the area of triangle ADQ will also relate to the area of triangle ADC.
8. Area of Triangle ADC:
- The area of triangle ADC is:
Area of △ADC=12×AD×h4
where h4 is the height from point D to line AC.
Hint: Since AD is parallel to BC, the heights can help in establishing relationships.
9. Final Relationships:
- From the properties of parallelograms and the triangles formed, we can conclude:
Area of △ADQ=Area of △ADC
and thus, by combining these relationships, we can find that:
Area of △ACP=Area of △DPQ
Hint: Use the relationships established in the previous steps to derive the final area relationships.
Conclusion:
The areas of triangles ACP and DPQ are equal due to the properties of the parallelogram and the relationships established through the points P and Q.
- Begin by sketching the parallelogram ABCD with vertices A, B, C, and D. Ensure that opposite sides are parallel and equal in length.
- Draw a line through point A that intersects line DC at point P and extends to intersect the line BC (produced) at point Q.
- Identify the triangles formed: Triangle ACP and Triangle BCP. Notice that both triangles share the base CP.
- The area of triangle ACP can be expressed as:
Area of △ACP=12×AC×h1
where h1 is the height from point P to line AC.
- Similarly, the area of triangle BCP can be expressed as:
Area of △BCP=12×BC×h2
where h2 is the height from point P to line BC.
- Since triangles ACP and BCP share the same height from point P to line AC and BC, we can conclude:
Area of △ACP=Area of △BCP
- Now consider triangle ADQ. The area can be expressed as:
Area of △ADQ=12×AD×h3
where h3 is the height from point Q to line AD.
- The area of triangle ADC is:
Area of △ADC=12×AD×h4
where h4 is the height from point D to line AC.
- From the properties of parallelograms and the triangles formed, we can conclude:
Area of △ADQ=Area of △ADC
and thus, by combining these relationships, we can find that:
Area of △ACP=Area of △DPQ
The areas of triangles ACP and DPQ are equal due to the properties of the parallelogram and the relationships established through the points P and Q.
Similar Questions
ABCD is a parallelogram; any line through A cuts DC at a point P and BC produced at Q. prove that triangle BCP is equal in area to triangle DPQ.
View SolutionABCD is a parallelogram and APQ is a straight line meeting BC at Pand DC produced at Q. prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.
View Solution
Knowledge Check
ABCD is a rhombus. A line passing through C cuts extended line AD and AB at Q and P respectively. If QD=12AB. Then find the ratio AB to PB.
 A2:1B1:2C1:1D3:1
A2:1B1:2C1:1D3:1ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given ∠BEF=80∘, find ∠ABC.
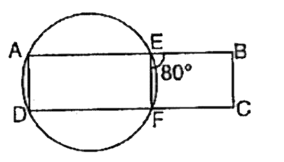 A100∘B40∘C80∘D104∘
A100∘B40∘C80∘D104∘
ABCD is a parallelogram and APQ is a straight line meeting BC at PandDC produced at Q. prove that the rectangle obtained by BPandDQ is equal to the rectangle contained by ABandBC.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionABCD is a parallelogram. P is a point on the side BC DP when produced meets AB produced at L. Prove that DPPL=DCBL (ii) DLDP=ALDC
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View Solution
