In ABC, D and E are points on sides AB and AC respectively such that AD×EC=AE×DB . Prove that DEBC .
To prove that DE∥BC given that AD⋅EC=AE⋅DB, we can follow these steps:
1. Given Information:
We are given that in triangle ABC, points D and E are on sides AB and AC respectively, such that:
AD⋅EC=AE⋅DB
2. Rearranging the Equation:
We can rearrange the given equation to express it in terms of ratios:
ADDB=AEEC
This follows from dividing both sides of the equation by DB⋅EC (assuming DB and EC are not zero).
3. Identifying Proportional Segments:
From the above ratio, we can see that:
ADAB=AEAC
Here, we recognize that AB=AD+DB and AC=AE+EC.
4. Using the Basic Proportionality Theorem:
According to the Basic Proportionality Theorem (or Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Since we have established the ratios:
ADDB=AEEC
This implies that line DE is parallel to line BC.
5. Conclusion:
Therefore, we conclude that:
DE∥BC
This completes the proof.
We are given that in triangle ABC, points D and E are on sides AB and AC respectively, such that:
AD⋅EC=AE⋅DB
We can rearrange the given equation to express it in terms of ratios:
ADDB=AEEC
This follows from dividing both sides of the equation by DB⋅EC (assuming DB and EC are not zero).
From the above ratio, we can see that:
ADAB=AEAC
Here, we recognize that AB=AD+DB and AC=AE+EC.
According to the Basic Proportionality Theorem (or Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Since we have established the ratios:
ADDB=AEEC
This implies that line DE is parallel to line BC.
Therefore, we conclude that:
DE∥BC
This completes the proof.
Topper's Solved these Questions
Similar Questions
D and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=4 , AE=8 , DB=x−4 , and EC=3x−19 , find x (ii) If AD=8 cm , AB=12cm and AE=12 cm , find CE . (iii) If AD=4 cm , DB=4.5 cm and AE=8 cm , find AC .
View Solution
Knowledge Check
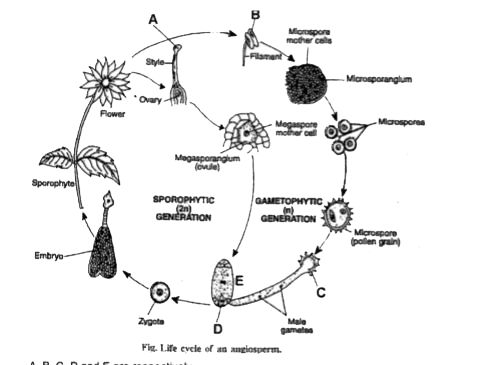
A, B, C, D and E are respectively -AStigma, Anther, Male gametophyte, Egg and Female gametophyteBStigma, Anther, Female gametophyte, Egg and Male gametophyteCStigma, Anther, Male gametophyte, Fertilized egg and Female gametophyteDStigma, Anther, Embryo sac, Egg and Female gametophyte
In a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=6 cm , DB=9 cm and AE=8 cm , find AC . (ii) If ADDB=34 and AC=15 cm , find AE . (iii) If ADDB=23 and AC=18 cm , find AE .
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=8x−7, DB=5x−3, AE=4x−3 and EC=(3x−1) , find the value of x . (ii) If AD=4x−3, AE=8x−7, BD=3x−1 and CE=5x−3 , find the volume x . (iii) If AD=2.5 cm , BD=3.0 cm and AE=3.75 cm , find the length of AC .
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=2 cm , AB=6 cm and AC=9 cm , find AE . (ii) If ADBD=45 and EC=2.5 cm , find AE . (iii) If AD=x , DB=x−2 , AE=x+2 and EC=x−1 , find the value of x .
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View Solution

