A rhombus is inscribed in the region common to the two circles x2+y2−4x−12=0 and x2+y2+4x−12=0 with two of its vertices on the line joining the centers of the circles. The area of the rhombus is
8√3 sq. units
4√3 sq. units
6√3 sq. units
none of these
The correct Answer is:A
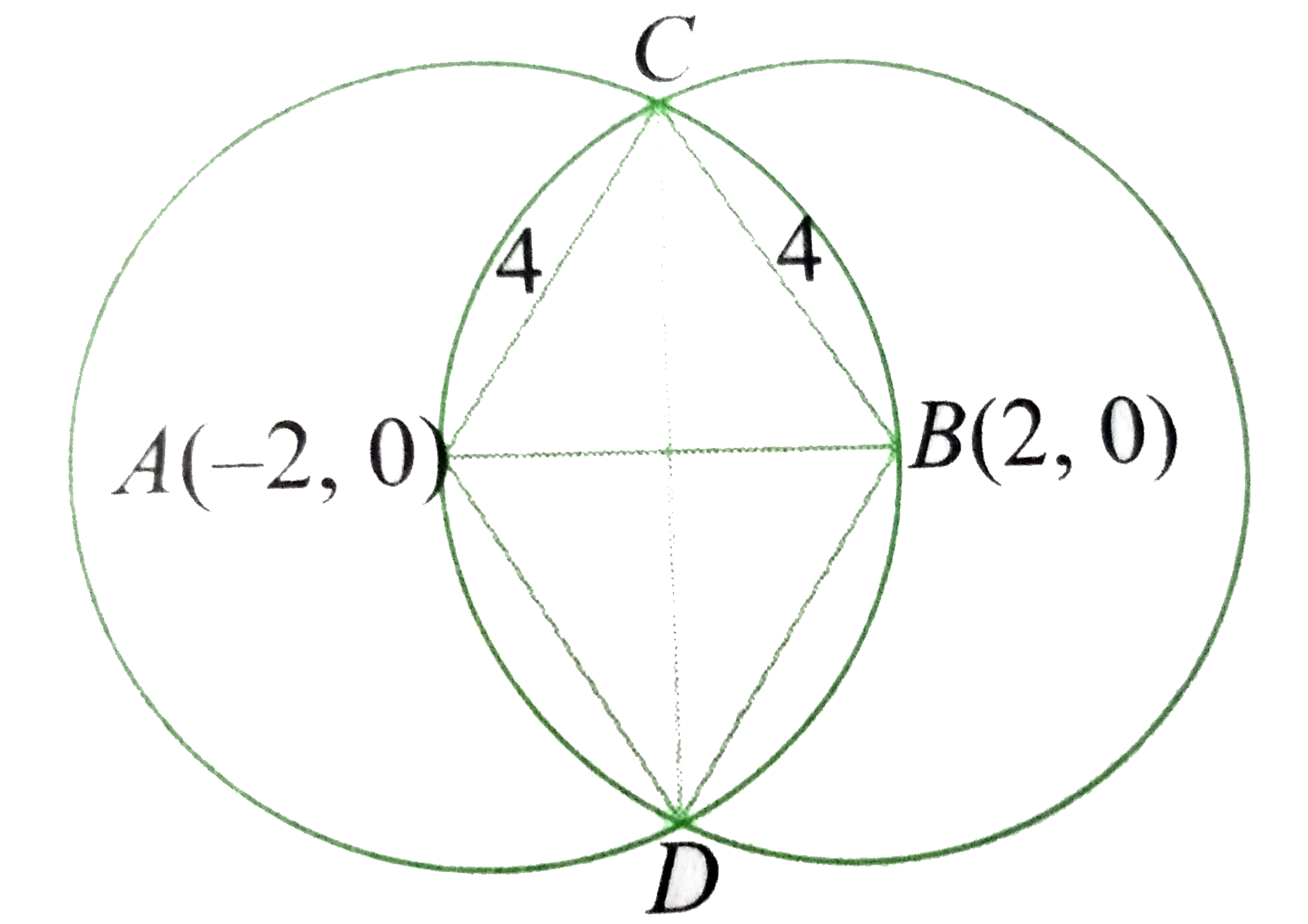
The circles are with centers (2,0) and (−2,0) and radius 4.
Therefore, the y-axis is their common chord.
ΔABC is equilateral. Hence,
Area of ADBC =2×√34(4)2=8√3
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Multiple)
Explore 25 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Comprehension)
Explore 46 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.6
Explore 5 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
A rhombus is inscribed in the region common to the two circles x2+y2−4x−12=0 and x2+y2+4x−12=0 with two of its vertices on the line joining the centers of the circles. The are of the rhombus is (A) 8√3 sq.units (B) 4√3 sq.units (C) 6√3 sq.units (D) none of these
View SolutionA rhombus is inscribed in the region common to the two circle x2+y2−4x−12=0andx+y−4x−12=012 its vertices on the line joining the centres of the circles. The area of the rhombous is?
View Solution
Knowledge Check
The two circles x2+y2−2x−3=0 and x2+y2−4x−6y−8=0 are such that
Athey touch each otherBthey intersect each otherCone lies inside the otherDeach lies outside the otherThe two circles x2+y2−2x−3=0 and x2+y2−4x−6y−8=0 are such that
Athey touch each otherBthey intersect each otherCone lies inside the otherDeach lies outside the otherThe number of common tangents to the circles x2+y2−4x−6y−12=0 and x2+y2+6x+18y+26=0, is
A3B4C1D2
The radical axis of the circles x2+y2+4x−6y=12 and x2+y2+2x−2y−1=0 divides the line segment joining the centres of the circles in the ratio
View SolutionThe circles x2+y2−4x−6y−12=0 and x2+y2+4x+6y+4=0
View SolutionThe circles x2+y2+6x+6y=0 and x2+y2−12x−12y=0
View SolutionThe number of common tangents of the circles x2+y2+4x+1=0 and x2+y2−2y−7=0, is
View SolutionFind the number of common tangents to the circles x2+y2−4x−6y−12=0 and
x2+y2+6x+18y+26=0
View Solution