If the distance of the point P(1,−2,1) from the plane x+2y−2z=α,whereα>0,is5, then the foot of the perpendicular from P to the place is a. (83,43,−73) b. (43,−43,13) c. (13,23,103) d. (23,−13,−53)

A

(83,43,−73)

B

(43,43,13)

C

(13,23,103)

D

(23,13,52)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Distance of point P from plane =5
∴ 5=∣∣∣1−4−2−α3∣∣∣
⇒ α=10
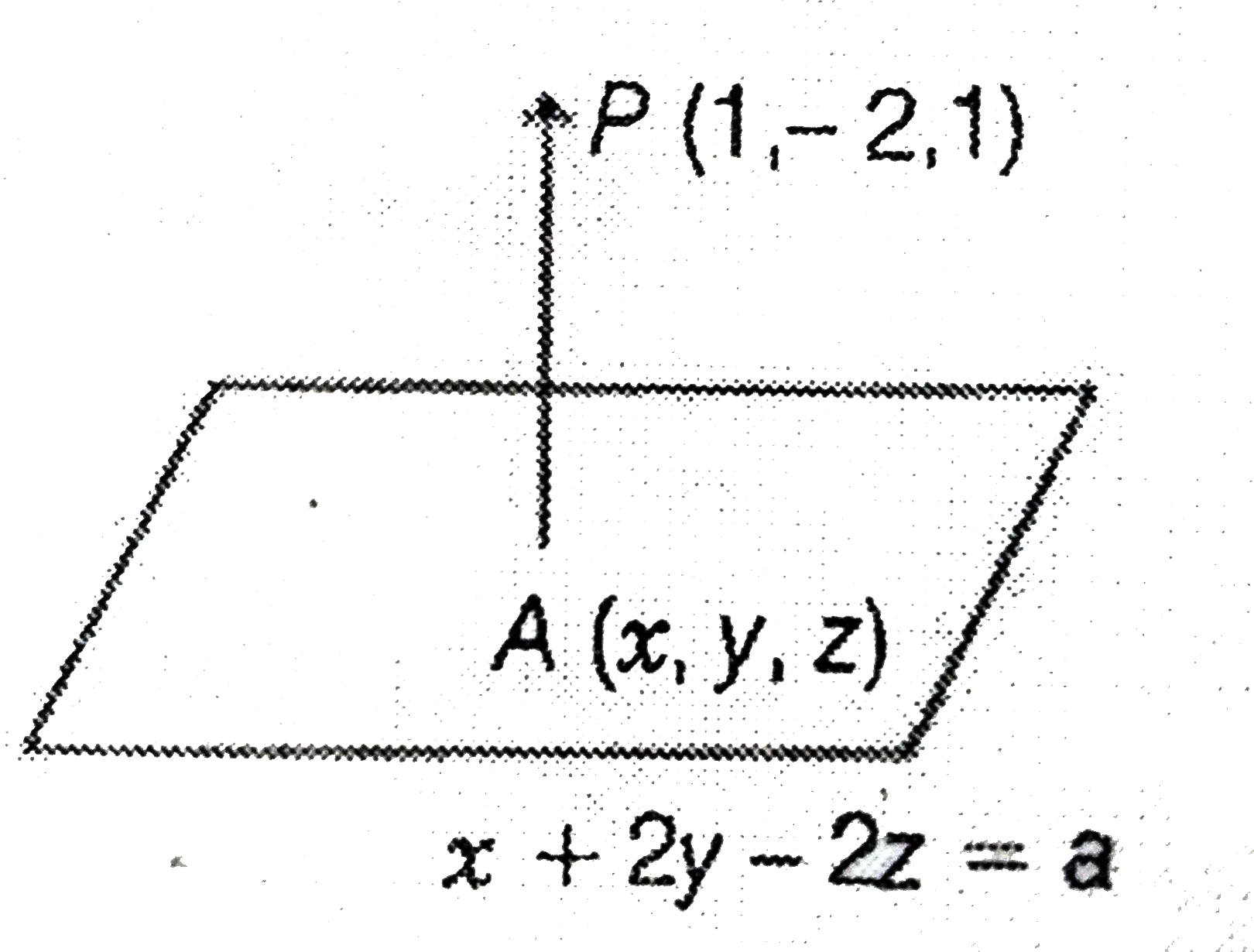
ocr_image
Foot of perpendicular
x−11=y+22=z−1−2=53
⇒ x=83,y=43,z=−73
Thus, the foot of the perpendicular is A(83,43,−73).

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Find the foot of perpendicular from (0, 2, 3) to the
    line x−32=y−12=z+43.

    A(-2, 3, 4)
    B(2, -1, 3)
    C(5, 3, -1)
    D(3, 2, -1)

  • The foot of perpendicular from (0,2,3) to the line x+35=y−12=z+43 is

    A(−2,3,4)
    B(2,−1,3)
    C(2,3,−1)
    D(3,2,−1)

  • The foot of the perpendicular drawn from point (2,-3,1) to the line x+12=y−33=z+2−1 is

    A(−2214,−314,−1314)
    B(−227,−314,−134)
    C(2214,314,1314)
    D(227,314,1314)