Consider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin, and OP and OR along the x-axis and the y-axis,respectively. The base OPQR of the pyramid is asqu are with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3.Then
the acute angle between OQ and OS is π3
the equation of the plane containing the ΔOQS is x−y=0
the length of the perpendicular from P to the plane containing the ΔOQS is 3√2
the perpendicular distance from O to the straight line containing RS is √152
The correct Answer is:B, C, D
Given, square base OP=OR=3
∴ P(3,0,0),R=(0,3,0)
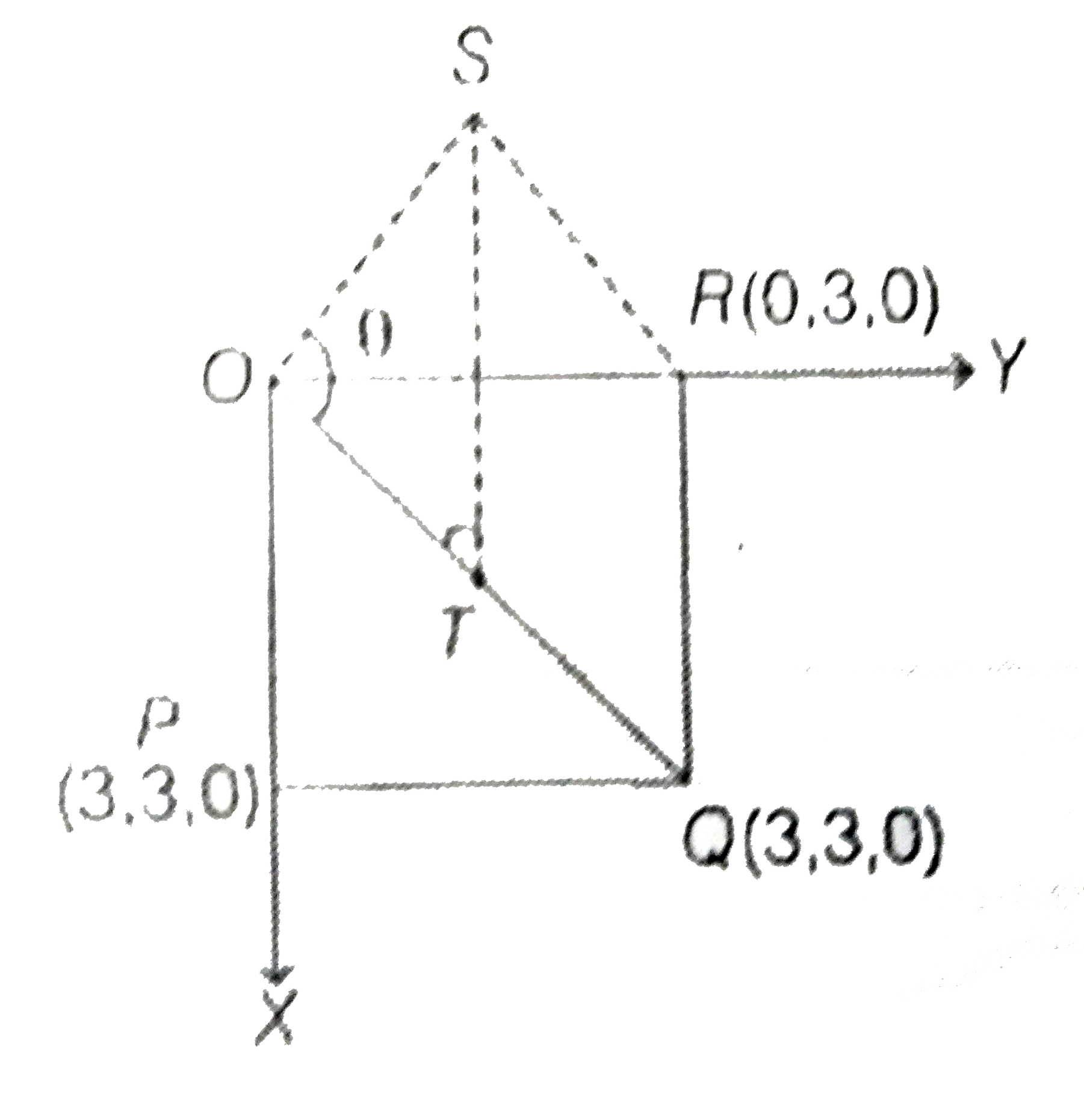
Also, mid-point of OQ is T(32,32,0).
Since, S is directly above the mid-point T of diagonal OQ and ST=3.
i.e. S(32,32,3)
Here, DR's of OQ(3,3,0) and DR's of OS(32,32,3).
∴cosθ=92+92√9+9+0√94+94+9=9√18.√272=1√3
∴ Option (a) is incorrect.
Now, equation of the plane containing the ΔOQS is
∣∣
∣
∣∣xyz3303/23/23∣∣
∣
∣∣=0⇒∣∣
∣
∣∣xyz110112∣∣
∣
∣∣=0
⇒ x(2−0)−y(2−0)+z(1−1)=0
⇒ 2x−2y=0 or x−y=0
∴ Option (b) is correct.
Now, length of the perpendicular from P(3,0,0) to the plane containing ΔOQS is |3−0|√1+1=3√2
∴ Option (c) is correct.
Here, equation of RS is
x−03/2=y−3−3/2=z−03=λ
⇒ x=32λ,y=−32λ+3,z=3λ
To find the distance from O(0,0,0) to RS.
Let M be the foot of perpendicular.
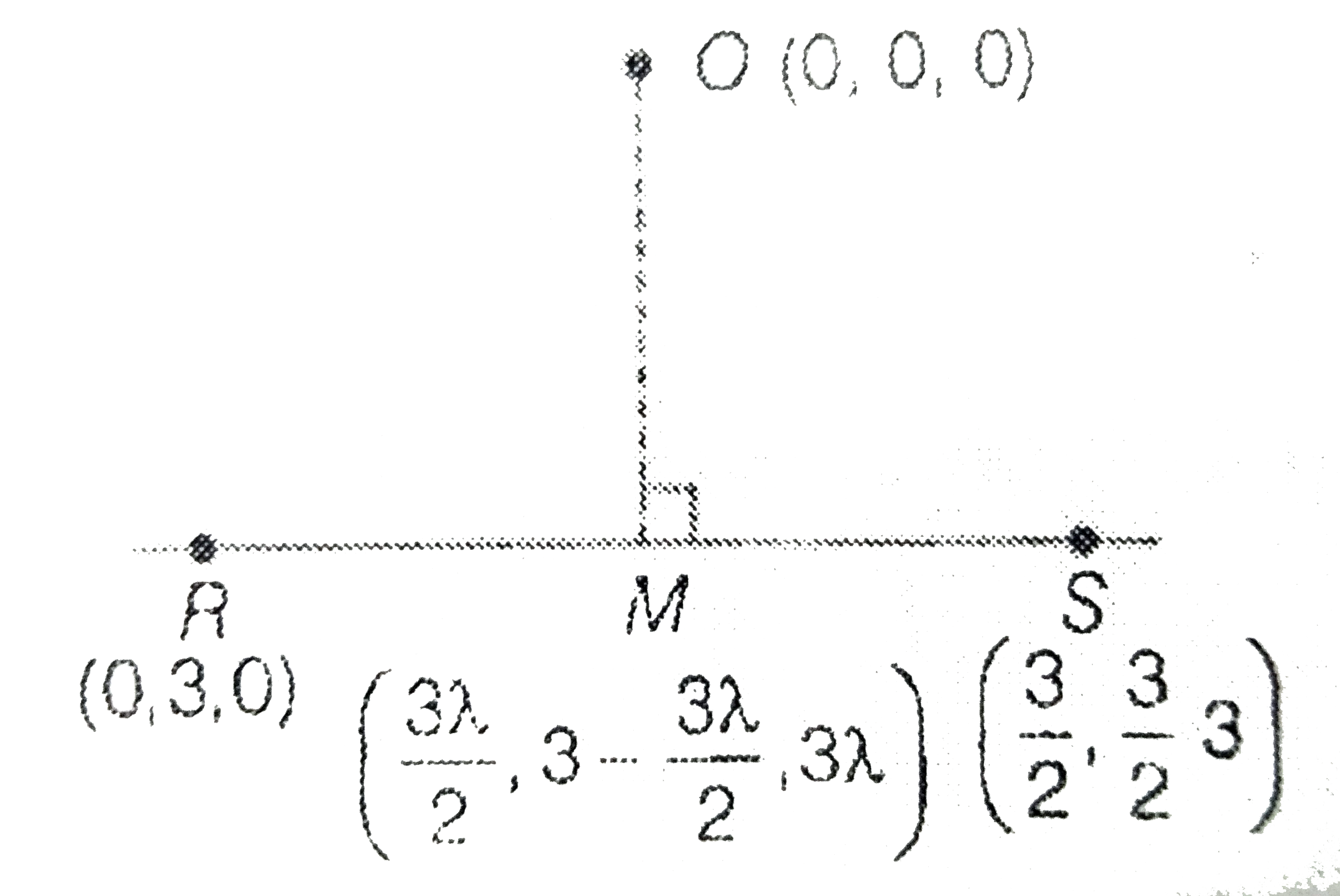
(3λ2,3−3λ2,3λ)(32,323)
∵ ¯¯¯¯¯¯¯OM⊥¯¯¯¯¯RS⇒¯¯¯¯¯¯¯OM.¯¯¯¯¯RS=0
⇒ 9λ4−32(3−3λ2)+3(3λ)=0⇒λ=13
∴M(12,52,1)⇒OM=√14+254+1=√304=√152
∴ Option (d) is correct.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Numerical Value)1videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Passage Based Problems)3videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question I (Only one correct option)49videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE20videos
PROPERTIES OF TRIANGLES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)8videos
APPLICATION OF DERIVATIVES
Similar Questions
Consider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
View SolutionConsider a pyamid OPQRS locaated in the first octant (x≥0,y≤0,z≤0) with O as origin , and OP an OR along the x-axis and y-axis respectively. The base OPQR of the pyramid is a square with OP=3 . The point S is directly above the mid-point T of the diagonal OQ such that TS=3 , Then , the angle between OQ and OS, is
View SolutionConsider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t)∣is
View SolutionA cube in the first octant has sides OP, OQ and OR of length 1, along the z-axis, y-axis and z-axis, respectively, where O(0, 0, 0) is the origin. Let the centre of the cube be at S(12.12,12) and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST, then the value of ∣∣(→p×→q)×(→r×→t)∣∣ is:
View SolutionIf a line OP through the origin O makes angles α,45∘and60∘ with x, y and z axis respectively then the direction cosines of OP are.
View SolutionIF O be the origin and OP makes angles 450and600 with the positive directionof x and y-axes respectively and OP=12 units find the coordinates of P.
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A, B moves on xandy axis respectively, then locus of mid point of AB is
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A,B moves on xandy axis respectively, then locus of mid point of AB is
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A,B moves on xandy axis respectively, then locus of mid point of AB is
View SolutionTwo point charges −q and +q/2 are situated at the origin and the point (a,0,0) respectively. The point along the X-axis where the electric field Vanishes is
View Solution


