The point P is the intersection of the straight line joining the points Q(2,3,5) and R(1,−1,4) with the plane 5x−4y−z=1. If S is the foot of the perpendicular drawn from the point T(2,1,4) to QR, then the length of the line segment PS is (A) 1√2 (B) √2 (C) 2 (D) 2√2
1√2
√2
2
2√2
The correct Answer is:A
PLAN It is based on two concepts one is intersection of straight line and plane and other is the foot of perpendicular from a point to the straight line.
Description of Situation
(i) If the staight line
x−x1a=y−y1b=z−z1c=λ

intersects the plane Ax+By+Cz+d=0.
Then, (aλ+x1,bλ+y1,cλ+z1) would satisfy
Ax+By+Cz+d=0
(ii) If A is the foot of perpendicular from P to l.
Then, (DR's of PA) is perpendicualr to DR's of l.
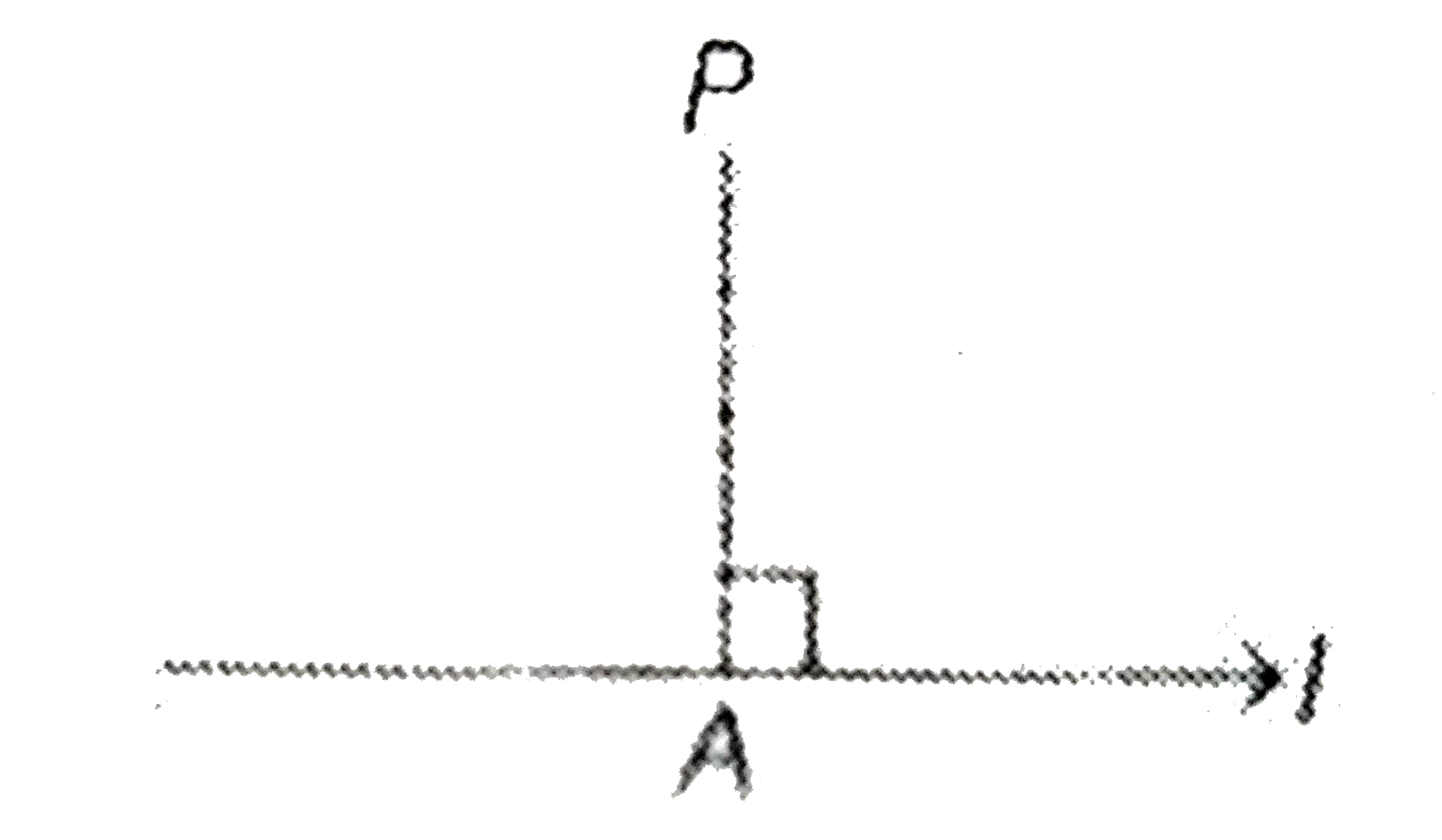
⇒ ¯¯¯¯¯¯PA.¯l=0
Equation of straight line QR, is
x+21−2=y−3−1−3=z−5−1
⇒ x−2−1=y−3−4=z−5−1
⇒ x−21=y−34=z−51=λ...(i)
∴P(λ+2,4λ+3,λ+5) must lie on 5x−4y−z=1
⇒ 5(λ+2)−4(4λ+3)−(λ+5)=1
⇒ 5λ+10−16λ−12−λ−5=1
⇒ −7−12λ=1
∴ λ=−23
or P(43,13,133)
Again, we can assume S from Eq. (i),
as S(μ+2,4μ+3,μ+5)
∴DR's of TS<μ+2−2,4μ+3−1,μ+5−4>
=<μ,4μ+2,μ+1>
and DR's of QR=<1,4,1>
Since, perpendicualr
∴ 1(μ)+4(4μ+2)+1(μ+1)=0
⇒ μ=−12 and S(32,1,92)
∴Length of PS=√(32−43)2+(1−13)2+(92−133)2=1√2
Topper's Solved these Questions
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (One or more than pne correct option)
5 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Numerical Value)
1 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Straight Line in Space and Shortest Distance Objective Question II (One or more than one correct option)
3 Videos
- PROPERTIES OF TRIANGLESBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE
20 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
Similar Questions
The point P is the intersection of the straight line joining the points Q(2,3,5) and R(1,−1,4) with the plane 5x−4y−z=1. If S is the foot of the perpendicular drawn from the point T(2,1,4) to QR, then the length of the line segment PS is (A) 1√2 (B) √2 (C) 2 (D) 2√2
View SolutionThe foot of the perpendicular from the point P(1,3,4) to the plane 2x-y+z+3=0 is
View Solution
Knowledge Check
The projection of the line segment joining the
Points (1, 2, 3) and (4, 5, 6) on the plane
2x+y+z=1 isA1B√3C5D6The foot of the perpendicular drawn from the point (1, 8, 4) on the line joining the points (0, -11, 4) and (2, -3, 1) is
A(4, 5, 2)B(4, 5, 2)C(4, -5, 2)D(4, 5,-2)A line joining the points (1,1,1) and (2,2,2) intersect the plane x+y+z=9 at the point
A(3,4,2)B(2,3,4)C(3,2,4)D(3,3,3)
The length of the perpendicular drawn from the point (5,4,−1) on the line x−12=y9=z5
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,2,1) to the line joining B(1,4,6)andC(5,4,4).
View SolutionThe foot of the perpendicular drawn from point (2,-3,1) to the line x+12=y−33=z+2−1 is
View SolutionThe point at which the line joining the points (2,−3,1)and(3,−4,−5) intersects the plane 2x+y+z=7 is
View SolutionThe foot of the perpendicular drawn form the point (4,2,3) to the line joining the points (1,−2,3)and(1,1,0) lies on the plane:
View Solution
