The length of the projection of the line segment joining the points (5,-1,4) and (4,-1,3) on the plane x+y+z=7 is
A
2√3
B
23
C
13
D
√23
Video Solution
Text Solution
The correct Answer is:D
length of projection of the line segment joining a1 and a2 on the plane r.n=d is ∣∣∣(a2−a1)×n|n|∣∣∣
Length of projection the line segment joining the points (5,-1,4) and (4,-1,3) on the plane x+y+z=7 is

AC=∣∣∣(a2−a1)×n|n|∣∣∣=∣∣(−ˆi−ˆk)×(ˆi+ˆj+ˆk)∣∣∣∣ˆi+ˆj+ˆk∣∣
AC=∣∣ˆi−ˆk∣∣√3⇒AC=√2√3=√23
Alternative Method
Clearly, DR's of AB are 4−5,−1+1,3−4,i.e.−1,0,−1 and DR's of normal to plane are 1,1,1.
Now, let θ be the angle between the line and plane, then θ is given by sinθ=|−1+0−1|√(−1)2+(−1)2√12+12+12
=2√2√3=(√23
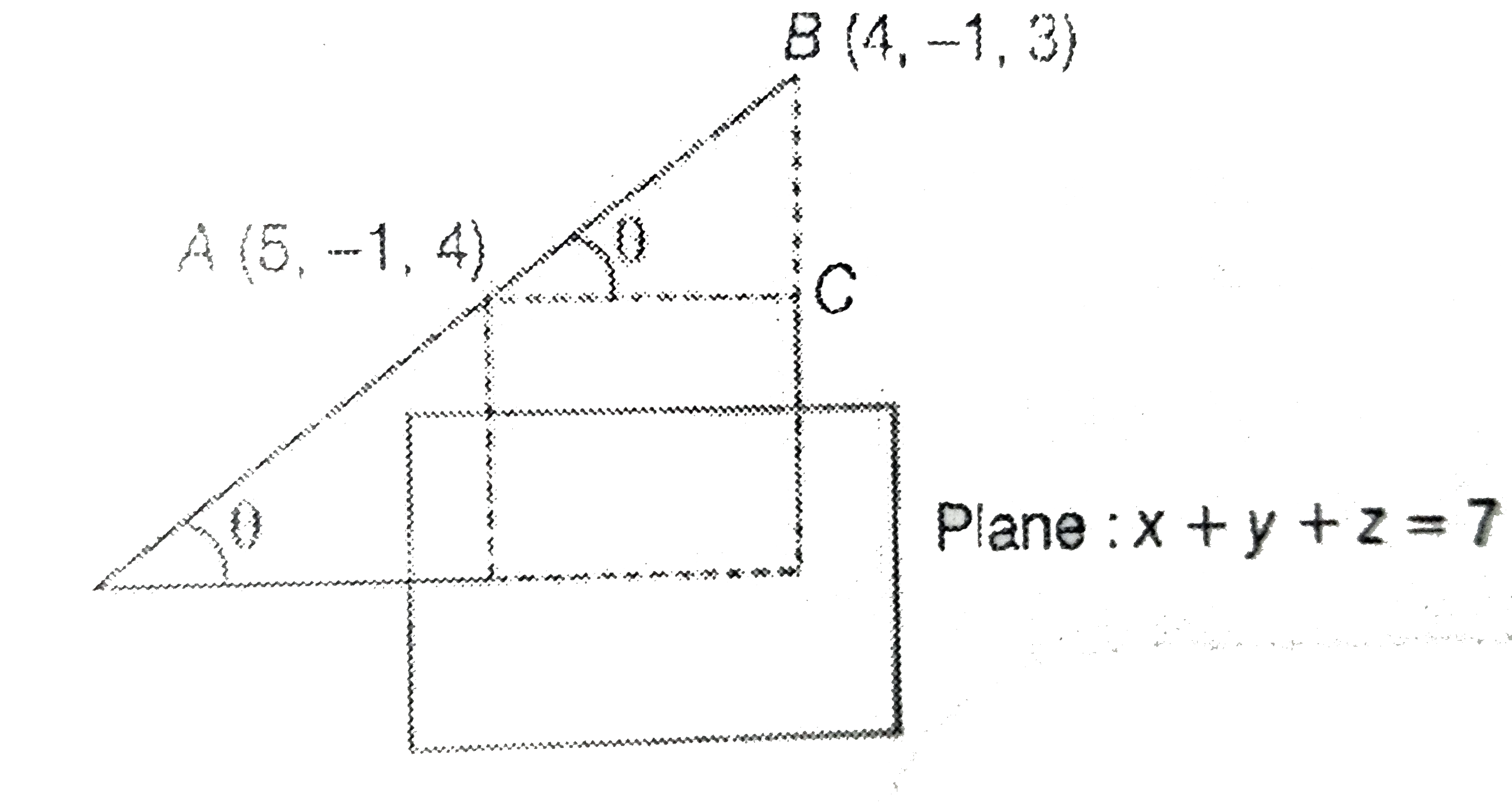
⇒sinθ=√23⇒cosθ=√1−sin2θ=√1−23=1√3
Clearly, length of projection =ABcosθ=√21√3 [∵AB=√2]
=√23
|
Topper's Solved these Questions
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (One or more than pne correct option)
5 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Numerical Value)
1 Video
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Straight Line in Space and Shortest Distance Objective Question II (One or more than one correct option)
3 Videos
- PROPERTIES OF TRIANGLESBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE
20 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
Similar Questions
Knowledge Check
The length of the projection of the line segment joining the points (5,−1,4) and (4,−1,3) on the plane x+y+z=7 is
A√23B23C√53D√43The length of projection, of the line segment joining the points (1,-1,0) and (-1,0,1) to the plane 2x+y+6z=1 is equal to
A√25541B√23741C√13741D√15541The projection of the line segment joining the
Points (1, 2, 3) and (4, 5, 6) on the plane
2x+y+z=1 isA1B√3C5D6
If the length of the projection of the line segment joining the points (1,2,−1) and (3,5,5) on the plane 3x−4y+12z=5 is equal to d units, then the value of 169d2 equal to
View SolutionWhat is length of the projection of line segment joining points (2,3) and (7,5) on x-axis.
View SolutionFind the length of the projection of the line segment joining (3,4,5) and (4,6,3) on the straight line ) :
x−42=y−53=z−66
View SolutionFind the projection of the line segment joining the points (3,3,5) and (5,4,3) on the line joining the points (2,-1,4) and (0,1,5)
View SolutionThe mid point of the line segment joining the points (−5,7)and(−1,3) is
View Solution
