A plane passing through three points (−λ2,1,)(1,−λ2,1),(1,1,λ2)1 also passes through (1,1,−1) then set consisting all the real value of λ is (A) {−√3,√3} (B) {3,−3} (C) {1} (D) {1,√3,−√3}

A

{√3,−√3}

B

{3,−3}

C

{1,−1}

D

{√3}

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

According to the question point (−λ2,1,1),(1,−λ2,1) and (1,1,−λ2) are coplanar with the point (-1, -1, 1), so
∣∣ ∣ ∣∣1−λ2 2 021−λ2 02 2−λ2−1∣∣ ∣ ∣∣=0
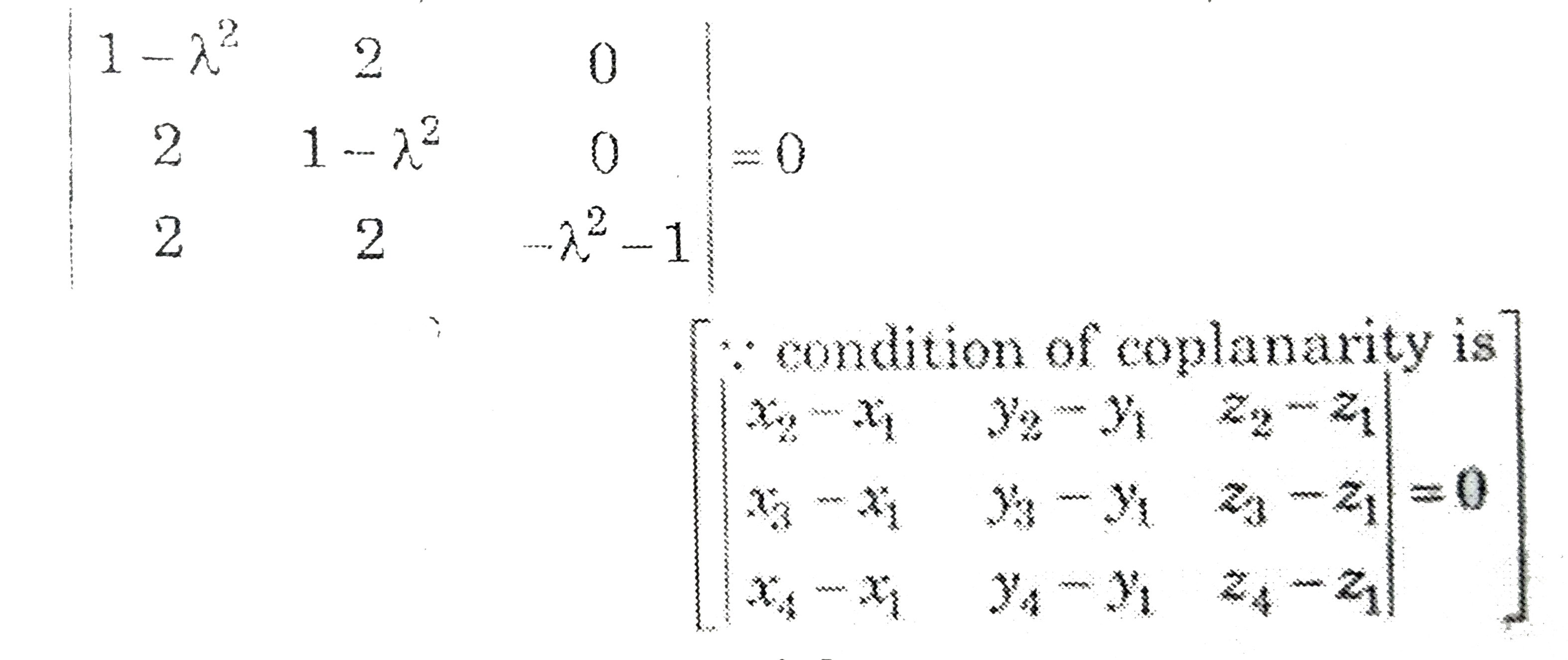
ocr_image
⇒ (−1−λ2)[(1−λ2)2−4]=0
⇒(1+λ2)[(1−λ2−2)(1−λ2+2)]=0
⇒ (1+λ2)2(3−λ2)=0
⇒ λ2=3 [∵1+λ2≠0∀λ∈R]
⇒ lambd±√3

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The equation of the plane passing through the points (1,2,3), (-1,4,2) and (3,1,1) is

    A5x+y+12z−23=0
    B5x+6y+2z−23=0
    Cx+6y+2z−13=0
    Dx+y+z−13=0

  • If the plane passing through the points (1,2,3),(2,3,1) and (3,1,2) is ax+by+cz=1 then a+2b+3c=

    A0
    B1
    C6
    D18

  • Let S be the set of all real values of λ such that a plane passing through the points (−λ2,1,1),(1,−λ2,1)and(1,1,−λ2) also passes through the point (−1,−1,1). Then, S is equal to:

    A{√3,−√3}
    B{3,3}
    C{1,−1}
    D{√3}