Two points A(7,0,6) and B(3,4,2) lie on a plane P1 and Plane P2:2x−5y=15 is perpendicular to the plane P1 and the pont (2,α,β) also lie on plane P1 . Then find the value of (2α,3β) (A) 12 (B) 17 (C) 5 (D) 7

A

17

B

7

C

5

D

12

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

According to given information, we have the following figure.
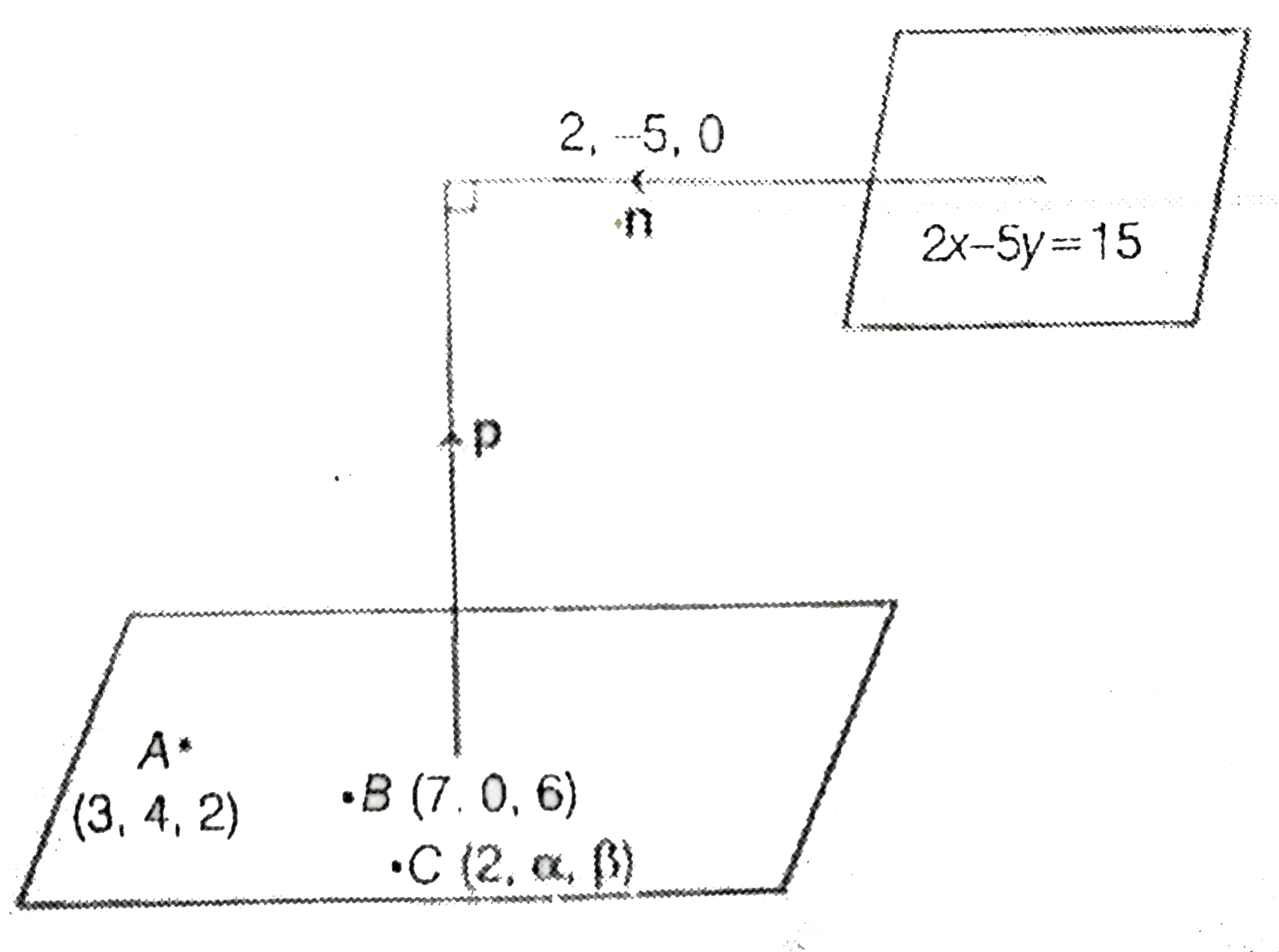
ocr_image
From figure, it is clear that
(AB×BC)=p and n=2ˆi−5ˆj+0ˆk
∴P=∣∣ ∣ ∣∣ ˆi ˆj ˆk 4−4 4−5 αβ−6∣∣ ∣ ∣∣
[∵AB=(7−3)ˆi+(0−4)ˆj+(6−2)ˆk
=4ˆi−4ˆj+4ˆk and BC=(2−7)ˆi+(α−0)ˆj+(β−6)ˆk
=−5ˆi+αˆj+(β−6)ˆk]
=ˆi(−4β+24−4α)−ˆj(4β−24+20)+ˆk(4α−20)
⇒P=(24−4α−4β)ˆi+ˆj(4−4β)+ˆk(4α−20)
Now, as the planes are perpendicular, therefore p.n=0
⇒((24−4α−4β)ˆi+(4−4β)ˆj+(4α−20)ˆk)
(2ˆi−5ˆj+0ˆk)=0
⇒2(24−4α−4β)−5(4−4β)+0=0
⇒8(6−α−β)−4(5−5β)=0
⇒12−2α−2β−5+5β=0⇒2α−3β=7

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the point (2,α,β) lies on the plane which passes through the points (3,4,2)and(7,0,6) and is perpendicular to the plane 2x−5y=15, then 2α−3β is equal to:

    A17
    B7
    C12
    D5

  • If the image of the point ( 1,-2,3) in the plane 2x+3y−z=7 is the point (α,β,γ), then the value of α+β+γ is equal to

    A−6
    B10
    C8
    D−4

  • A plane P = 0 passing through the point (1, 1, 1) is perpendicular to the planes 2x−y+2z=5 and 3x+6y−2z=7. If the distance of the point (1, 2, 3) from the plane P = 0 is k units, then the value of 34k2 is equal to

    A8√17
    B16
    C64
    D128