A long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
2v0ln(r/R2)ln(R1/R2)
v02ln(r/R2)(R1/R2)
v0ln(r/R2)(R1/R2)
2v03ln(r/R2)ln(R1/R2)
The correct Answer is:C
Viscous force G=−η(2πrl)dvdr,
where l = length of the cylinder
drr=−(2πηlF)dv
∫R2R1drr=−∫vv02πηlFdv⇒ln(R2R1)=2πηlFv0 ...(i)
Suppose velocity of liquid at a distacne r is v,
∫rR1drr=−∫vv02πηlFdv⇒lnrR1=2πηlF(v0−v) ...(ii)
ln(R2r)=2πηlFv
On solving eqs. (i) and (ii),
v=v0ln(R2/r)ln(R2/R1)⇒v=v0ln(r/R2)ln(R1/R2)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-1 CONCEPT BUILDER
59 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
Similar Questions
A long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionA cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
View Solution
Knowledge Check
A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of theseMoment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
A12MR2BMR2C23MR2D25MR2
A cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.

View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electic field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
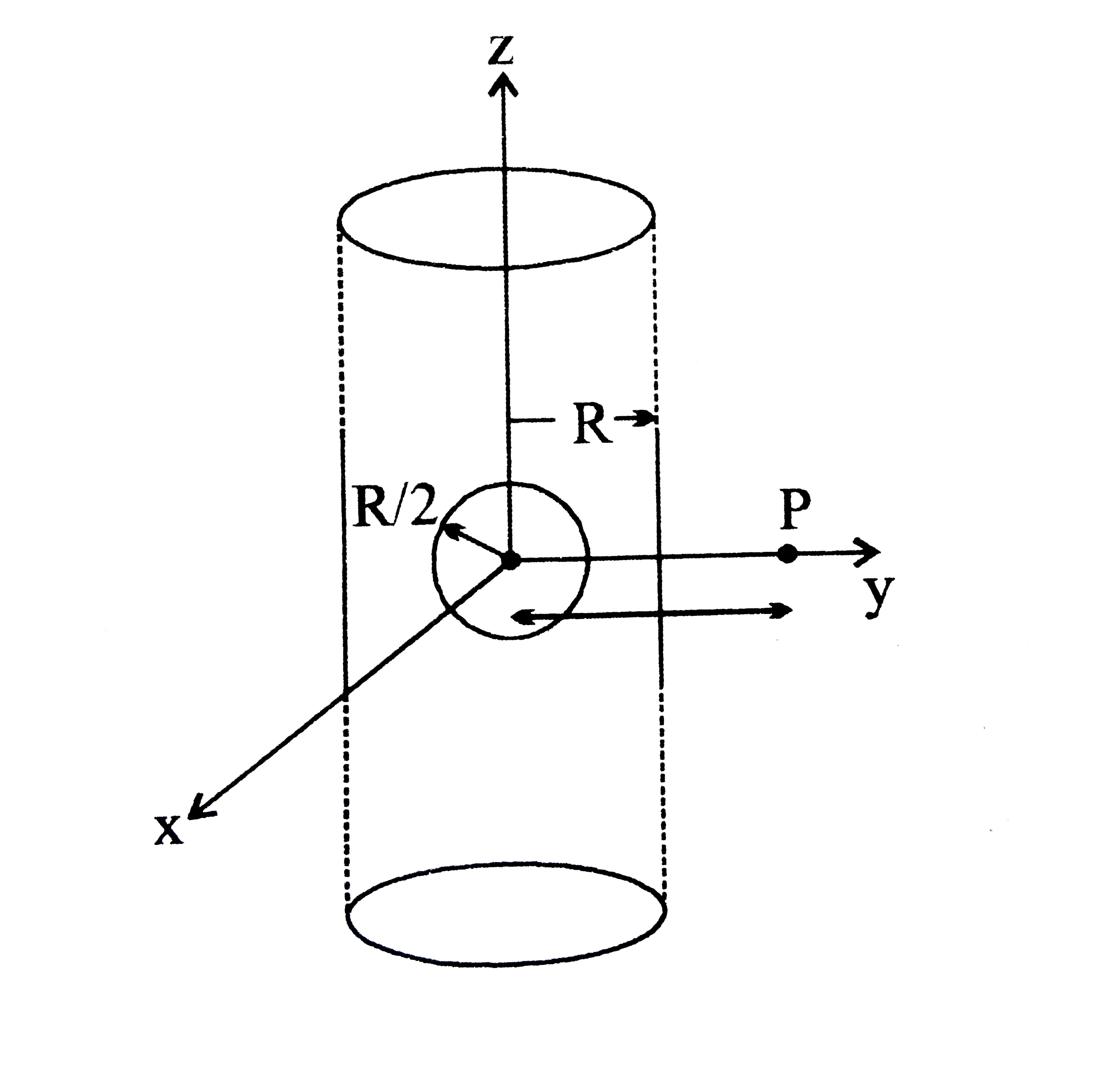 .
.
View SolutionA dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
View SolutionThe radius of a cylinder is r and heigth is h. Find its volume.
View SolutionThe horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1figure. The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder) , if the height of the fluid is equal to h.

View SolutionA long light thread is wond partly around cylinder of radius r and mass m partly on a simialr cylinder but free to turn about a fixed axis. The movable one is allowed to fall from rest. Find the velocity of the cylinder as a functiono of the height h through which it has fallen. Does the cylinder fall without slipping?
View Solution
