The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1figure. The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder) , if the height of the fluid is equal to h.

Step by step video & image solution for The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R_(1) over which a round closed cylinder is mounted, whose radius R_(2) gt R_(1)figure. The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is rho. find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder) , if the height of the fluid is equal to h. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:practice Exercise 7.1
Explore 10 Videos
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:Practice Exercise 7.2
Explore 8 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Unsolved Numerical
Explore 94 Videos
Similar Questions
The horizontal bottom of wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1 (figure). The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is ρ. Find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder), if the height of the fluid is equal to h.

View SolutionA long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View Solution
Knowledge Check
Let E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
AE1<E2 if r1<r2<RBE1>E2 if R<r1<r2CE1>E2, if r1=R−E,r2=R+E (E is positive constant <R )DAll of the aboveA tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
A4πηlV0B2πηlV0CπηlV0D23πηlV0If σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
AσR∈0krBσr∈0kRCσ∈0kDσ2R∈0kr
Three spheres of radius 'r' are kept inside a cuylinder such that two of the speres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder .Find the volume of the cylinder .
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
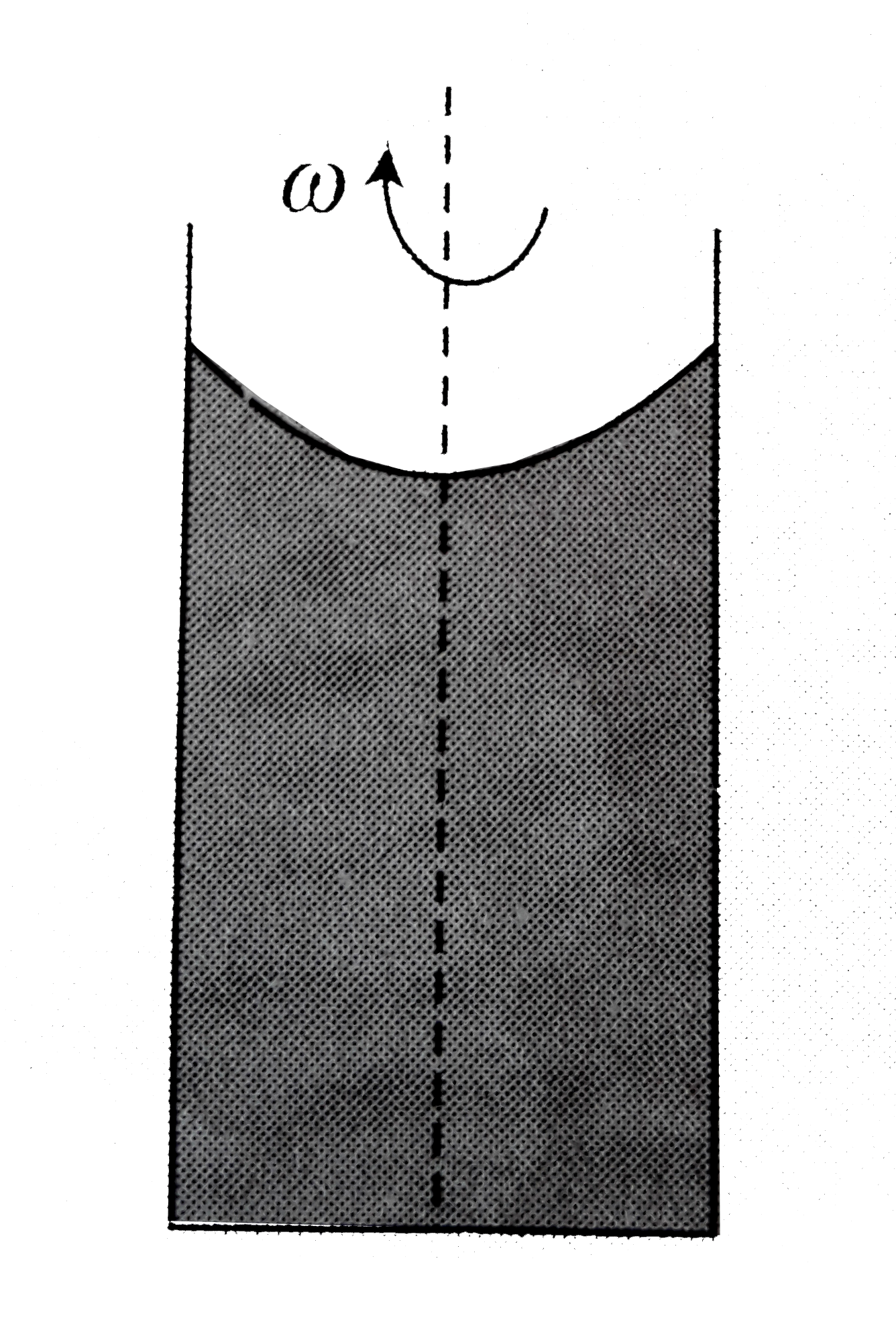 .
.
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View Solution

