ABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ABD=θ,Bc=pandCD=q, then AB is equal to
A
((p2+q2))sinθpcosθ+qsinθ
B
p2+q2cosθpcosθ+qsinθ
C
p2+q2p2cosθ+q2sinθ
D
q(p2+q2)(p2cosθ+q2sinθ)2
Video Solution
Text Solution
The correct Answer is:A
Applying sine rule in ΔABD,
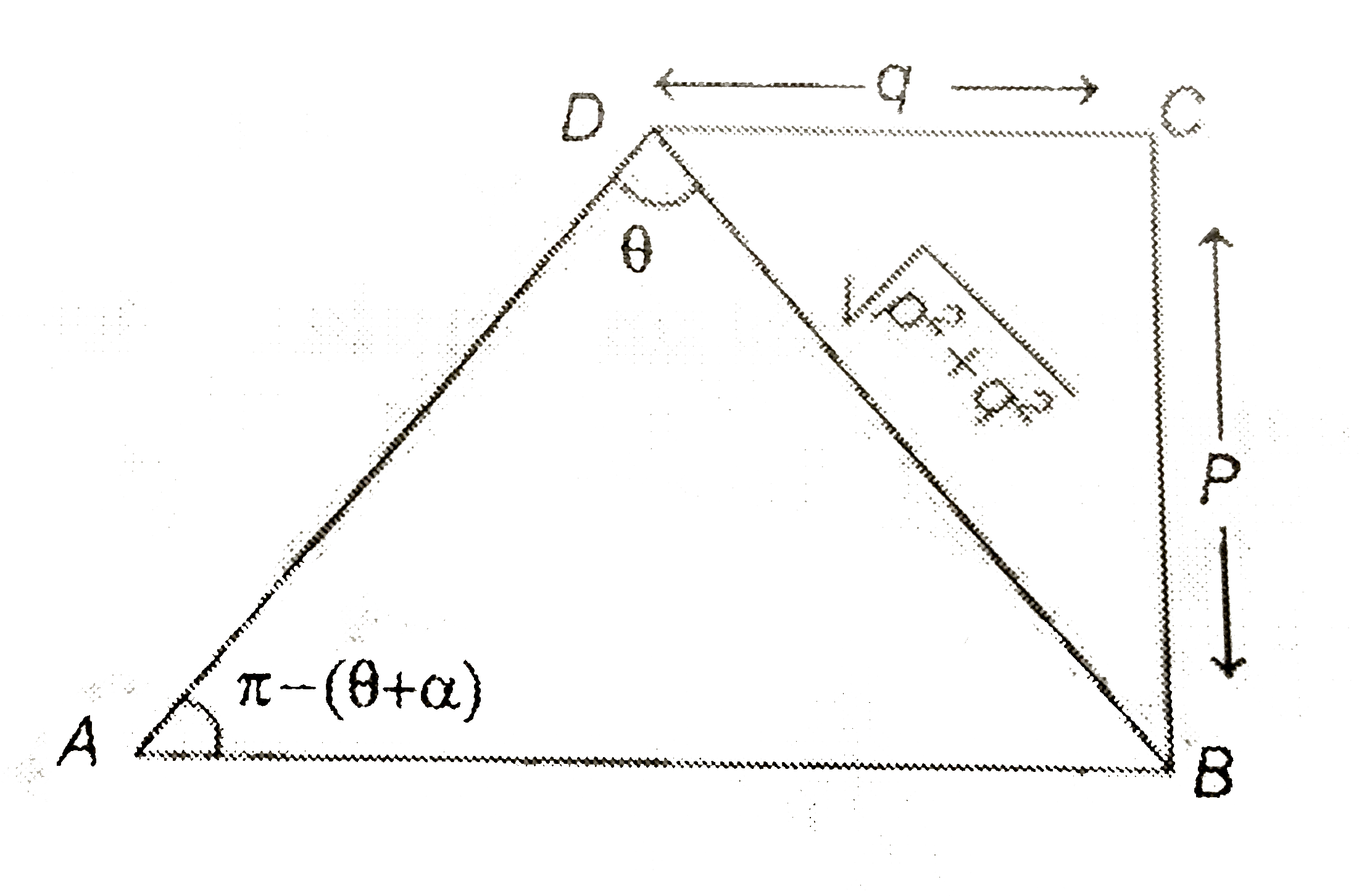
ABsinθ=√p2+q2sin{π−(θ+α)}
⇒ABsinθ=√p2+q2sin(θ+α)
⇒AB=√p2+q2sinθsinθcosα+cosθsinα[∴cosα=q√p2+q2]
=(p2+a2sinθ)pcos0+qsinθ
Alternate Solotion
Let AB=x

In ΔDAM,tan(πθ−α)=px−q
⇒tan(θ+α)=pq−x
⇒q−xpcot(θ+α)
⇒x=q−pcos(θ+α)
=p−q(cotθcotα−1cotα+cotθ)=[∴cotα=qp]
=q−p⎛⎝qpcotθ−1qp+cotθ⎞⎠=q−p(qcotθ−pq+pcotθ)
=q−p(qcosθ−psinθqsinθ+pcosθ)
⇒x=q2sinθ+qpcosθ−pqcosθ+p2sinθpcosθ+qsinθ
⇒AB=(p2+q2)pcosθ+qsinθ
|
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBook:IIT JEE PREVIOUS YEARChapter: PROPERTIES OF TRIANGLESExercise:APPLICATIONS OF AREA, NAPIERS ANALOGY AND SOLUTION OF A TRIANGLE
Explore 17 Videos
- PROPERTIES OF TRIANGLESBook:IIT JEE PREVIOUS YEARChapter: PROPERTIES OF TRIANGLESExercise:CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE
Explore 20 Videos
- 3D GeometryBook:IIT JEE PREVIOUS YEARChapter:3D GeometryExercise:Equation of Plane Objective Question II (Integer Answer Type Question)
Explore 1 Video
Similar Questions
Knowledge Check
ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. if ∠ADB=θ,BC=p and CD=q, then AB is equal to
A((p2+q2))sinθpcosθ+qsinθBp2+q2cosθpcosθ+qsinθCp2+q2p2cosθ+q2sinθDq(p2+q2)(p2cosθ+q2sinθ)2ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
Ap2+q2cosθpcosθ+qsinθBp2+q2p2cosθ+q2sinθC(p2+q2)cosθ(pcosθ+qsinθ)2D(p2+q2)sinθpcosθ+qsinθABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ADB=θ,Bc=pandCD=q, then AB is equal to
A(p2+q2sinθpcosθ+qsinθB(p2+q2)cosθpcosθ+qsinthetCp2+q2p2cosθ+q2sinθD(p2+q2)sinθ(pcosθ+qsinθ)
ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
View SolutionABCD is a trapezium with ∠A=90∘andAB parallel to CD. Then ∠B is :
View SolutionABCD is a trapezium with ∠A=90∘andAB parallel to CD. Then ∠B is :
View SolutionABCD is a trapezium such that AB and DC are parallel and BC is perpendicular to them. If BC=1 cm, CD=2 cm and ∠ADB=45∘, then the lengths of AB is (in cm)
View SolutionABCD is a trapezium such that AB, DC is parallel and BC is perpendicular to them. If angle (DAB) = 45∘ , BC = 2 cm and CD = 3 cm, then find the length of AB?
View Solution

