Let ABC be a triangle with incentre I and inradius r. Let D, E, F be the feet of the perpendiculars from I to the sides BC, CA and AB, respectively, If r1, r2 and r3 are the radii of circles inscribed in the quadrilaterls AFIE, BDIF and CEID respectively, then prove that r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
Video Solution
Text Solution
The quadrilateral HEKJ is a square, because all four angles are right angles and JK = JH.
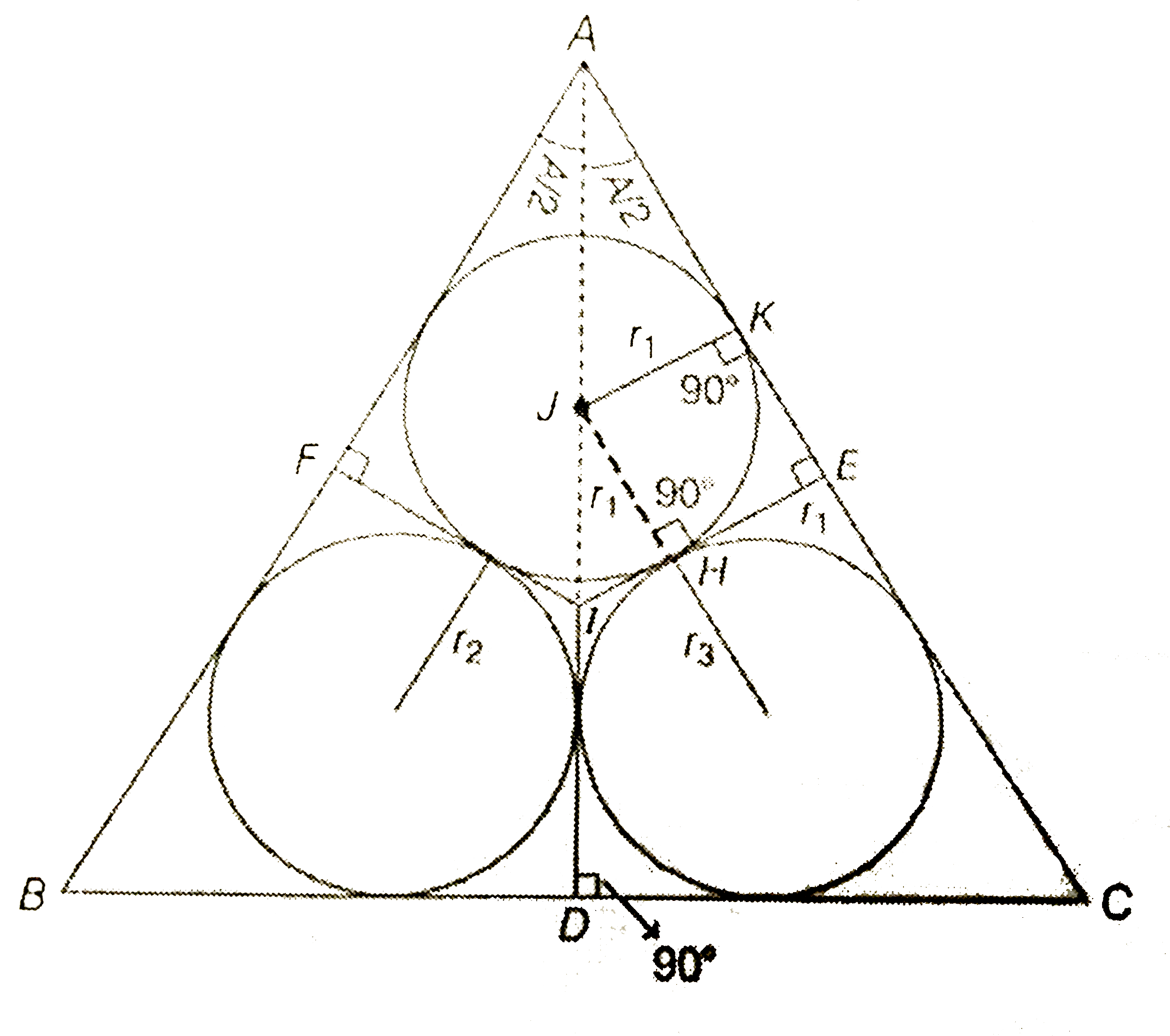
therefore, HE=JK=r1 and IE=r [given]
⇒ IH=r−r1
Now, in right angled ΔIHJ,∠JIH=π/2−A/2
[∵∠IEA=90∘,∠IAE=A/2 and ∠JIH=∠AIE]
In ΔJIH
tan(π2−A2)=r1r−r1⇒cotC2=r2r=r2
Similarly, cotB2=r2r−r2 and cotC2=r3r−r3
On adding above results, we get
cotA/2+cotB/2+cotC/2=cotA/2cotB/2cotC/2
⇒r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
|
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - APPLICATIONS OF AREA, NAPIERS ANALOGY AND SOLUTION OF A TRIANGLE
17 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)
1 Video
Similar Questions
Knowledge Check
If rr1=r2r3, then
AA=90∘BB=90∘CC =90∘Dnone of theseIf r1,r2,r3 are radii of the escribed circles of a triangle ABC and r it the radius of its incircle, then the root(s) of the equation x2−r(r1r2+r2r3+r3r1)x+(r1r2r3−1)=0 is/are :
Ar1Br2+r3C1Dr1r2r3−1If r1,r2,r3 are radii of the escribed circles of a triangle ABC and r it the radius of its incircle, then the root(s) of the equation x2−r(r1r2+r2r3+r3r1)x+(r1r2r3−1)=0 is/are :
Ar1Br2+r3C1Dr1r2r3−1
