The equations of two sides of a triangle are 3x−2y+6=0 and 4x+5y−20 and the orthocentre is (1,1). Find the equation of the third side.
122y-26y=0
26x-1675=0
122y+26x+165=0
26x+61y+1675=0
The correct Answer is:B
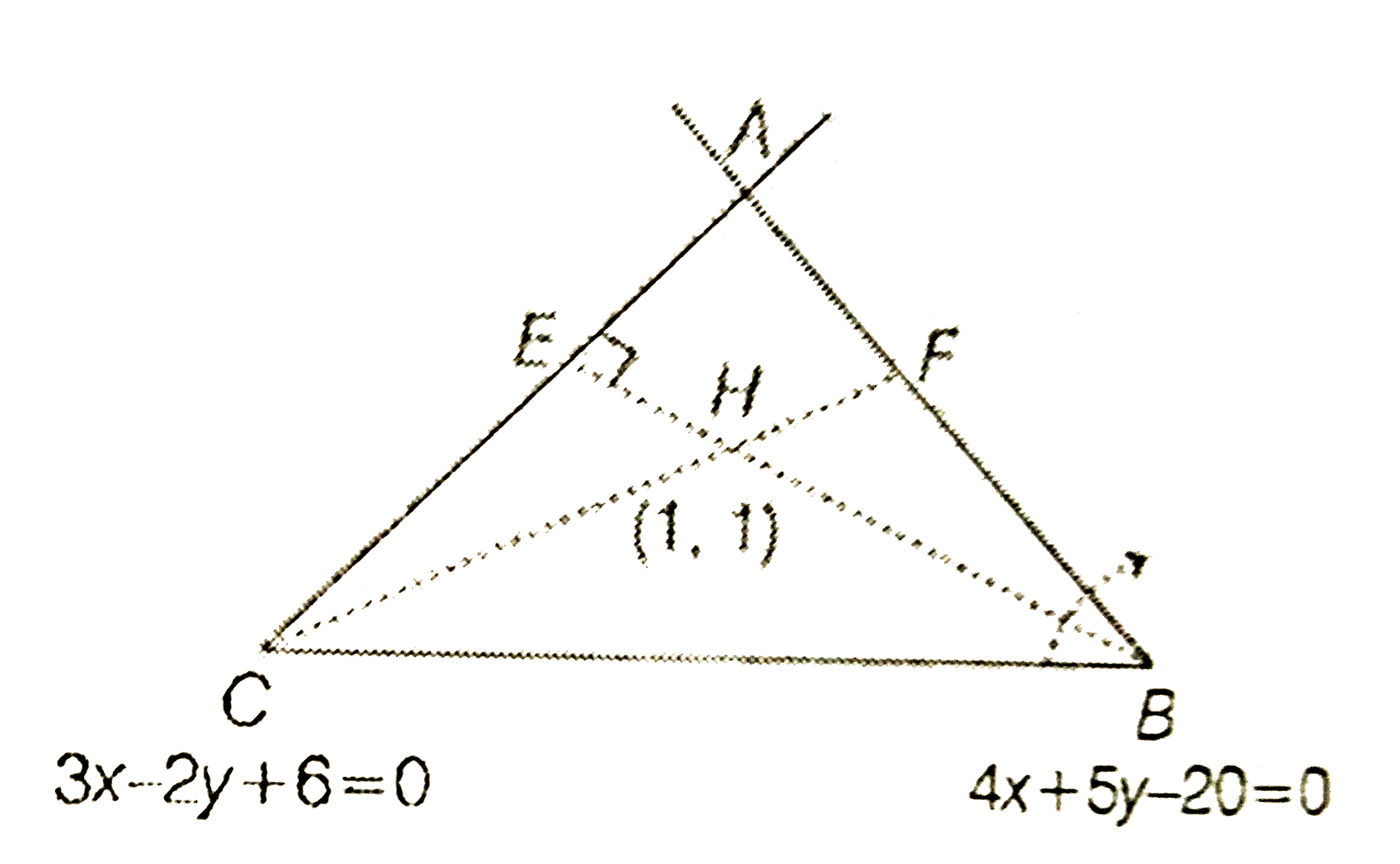
Let equation of AB bd 4x-5y-20=0 and AC be 3x-3y+6=0
Clearly, slope of AC=32
[∵ slope of ax + by +c = 0 is −ab]
∴ Slope of altitude BH, which is perpendicular to AC=−23 (∵mBH=−1mAC)
Equation of BH is given by y−y1=m(x−x1)
Here, m=−23,x1=1 and y1=1
∴ y−1=−23(x−1)
⇒2x+3y−5=0
Now, equation of AB is 4x+5y-20=0 and equation of BH is 2x+3y-5=0
Sloving these, we get point of intersection (i.e. coordinates of B)
4x+5y−20=04x+6y−10=0}⇒y=−10
On substituting y = -10 in 2x + 3y - 5 = 0, we get x=352)
∴ B(352,−10)
Solving 4x+5y-20=0 and 3x-2y+6=0, we get coordinate of A.
12x+15y−60=012x−8y+24=0}⇒23y=84
⇒ y=8423⇒x=1023
∴ A(1023,8423)
Now, slpe of AH=(y2−y1x2−x1)=⎛⎝8423−11023−1⎞⎠=61−13
∵ BC is perpendicular to AH.
∴Slope of BC is 1361 (∵mBC=−1mAH)
Now, equation of line BC is given by y−y1=m1(x−x1), Where (x1,y1) are coordinates of B.
∴ y−(−10)=1361(x−352)
⇒ y+10=1361×2(2x−35)
⇒ 122y+1220=26x−455
⇒ 26x−122y−−1675=0
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBook:IIT JEE PREVIOUS YEARChapter: PROPERTIES OF TRIANGLESExercise:APPLICATIONS OF AREA, NAPIERS ANALOGY AND SOLUTION OF A TRIANGLE
Explore 17 Videos
- 3D GeometryBook:IIT JEE PREVIOUS YEARChapter:3D GeometryExercise:Equation of Plane Objective Question II (Integer Answer Type Question)
Explore 1 Video
Similar Questions
The equations of two sides of a triangle are 3x−2y+6=0 and 4x+5y−20 and the orthocentre is (1,1). Find the equation of the third side.
View Solutionnd (, The eqn of two sides of a triangle are 3x-2y + 6-0 and 4x + 5y = 20 and the orthocentre is (1,1). Find the equation of the thired side.
View Solution
Knowledge Check
If the equations of three sides of a triangle are x+y=1,3x+5y=2andx−y=0 then the orthocentre of the triangle lies on the line/lines
A5x−3y=1B5y−3x=1C2x−3y=1D5x−3y=2
Let equation of two sides of a triangle are 4x+5y=20 and 3x−2y+6=0 If orthocentre of triangle is (1,1) then the equation of third side of triangle is (a) y+10=−1361(x+352) (2) y+10=−1361(x−352) (3) y+10=1361(x−352) (4) y−10=1361(x−352)
View SolutionThe equations of two sides of a square are 3x+4y−5=0and3x+4y−15=0 and (6, 5) is a point on the third side. Find the equation of the third side and the remaining side.
View SolutionIf two sides of a triangle lie along 3x2−5xy+2y2=0 and its orthocenter is (2,1) then the equation to the third side is
View SolutionThe equations of two sides of a square are 3x+4y−5=0and3x+4y−15=0. The third side has a point (6, 5) on it. Find the equation of this third side and the remaining side of the square.
View Solution9.y If two sides of a triangle are represented by x2_7xy+6y2=0 and the centroid is (1,0) then the equation of third side is
View SolutionIf two sides of a triangle are represented by x2_7xy+6y2=0 and the centroid is (1,0) then the equation of third side is
View SolutionThe equations of two sides of a triangle are 3x−2y+6=0and4x+5y−20=0 it the rauations of sides AB and AC of triangle ABC be = 0 and is (1, 1). Find the equation of the third side.
View Solution

