In a ΔPQR, Let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE (a) ∠QPR=45∘ (b) The area of the ΔPQR is 25√3 and ∠QRP=120∘ (c) The radius of the incircle of the ΔPQR is 10√3−15 (d) The area of the circumcircle of the ΔPQR is100π

A

∠QPR=45∘

B

The area of the ΔPQR is 25√3 and ∠QRP=120∘

C

The radius of the incircle of the ΔPQR is 10√3−15

D

The area of the circumcircle of the ΔPQR is100π

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B, C, D

We have,
In ΔPQR
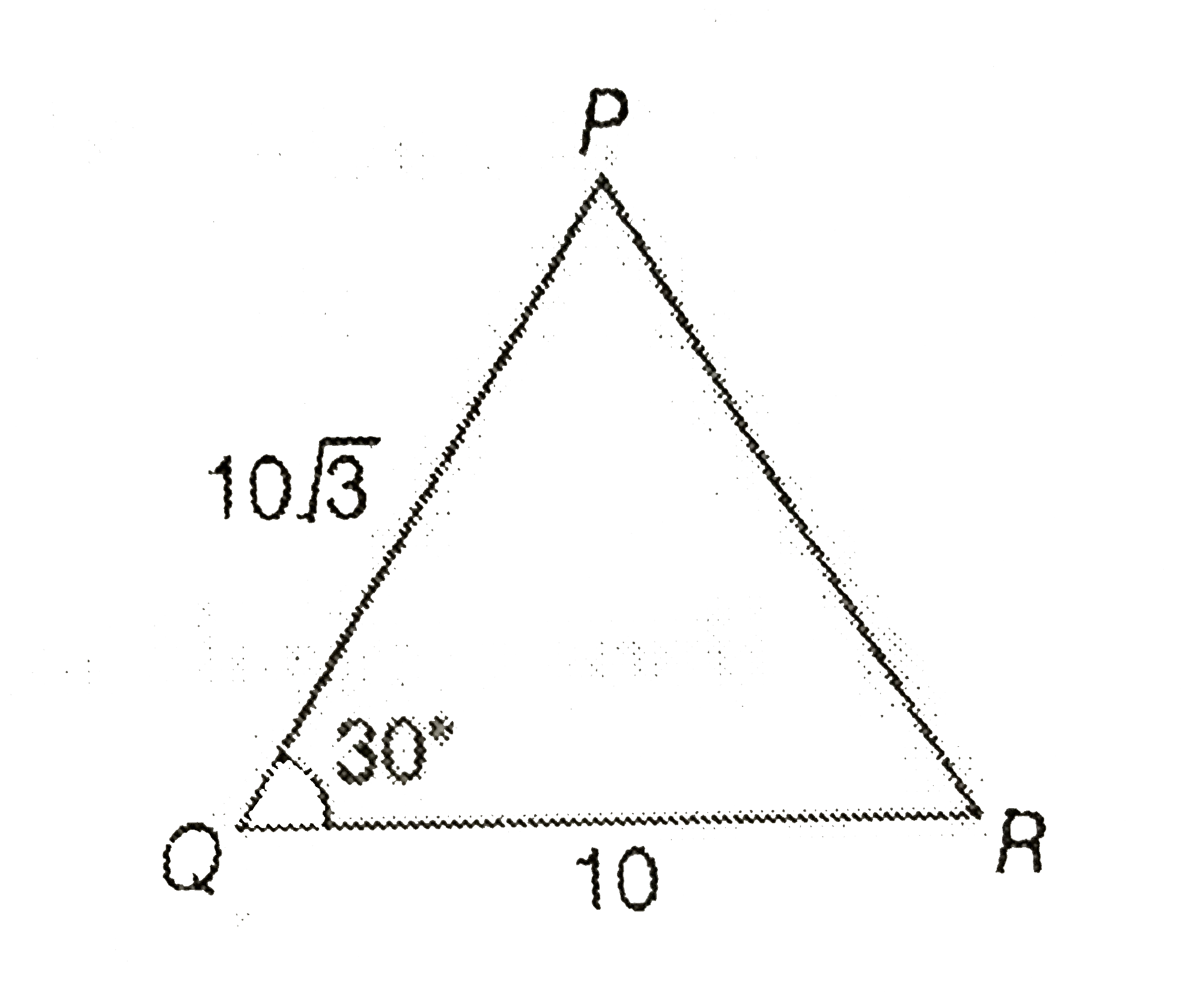
ocr_image
∠PQR=30∘
PQ=10√3
QR=10
By cosine rule
cos30∘=PQ2+QR2−PR22PQ QR
⇒ √32=300+100−PR2200√3
⇒ 300=300+100−PR2
⇒ PR=10
Since, PR=QR=10
∠PQR=30∘ and ∠QRP=120∘
=12×10√3×10×12=25√3
Radius of incircle of
ΔPQR=Area of ΔPQRSemi⋅perimtre of ΔPQR
i.e. r=Δs=25√310√3+10+102=25√35(√3+2)
⇒ r=5√3(2−√3)
=10√3−15
and radius of circumcircle (R)=abc4Δ=10√3×10×104×25√3=10
∴ Area of ci9rcumcircle of
ΔPQR=πR2=100π
Hence, option (b), (c ) and (d) are correct answer.

Updated on:21/07/2023
|
Class 12MATHS PROPERTIES OF TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?

    A∠QPR=45∘
    BThe area of the triangle PQR is 25√3and∠QRP=120∘
    CThe radius of the incircle of the triangle PQR is 10√3−15
    DThe area of the circumcircle of the triangle PQR is 100π

  • Which of the following statements (s) is/are TRUE ?
    I. √11+√7<√10+√8
    II. √17+√11>√15+√13

    AOnly I
    BOnly II
    CBoth I and II
    DNeither I nor II

  • Let ΔPQR be a triangle Let →a=¯¯¯¯¯¯QR,→b=¯¯¯¯¯¯RPand→c=¯¯¯¯¯¯PQif|→a|=12,∣∣→b∣∣=4√3and→b.→c=24,then which of the following is (are ) true ?

    A|→c|22−|→a|=12
    B|→c|22−|→a|=30
    C∣∣→a×→b+→c×→a∣∣=48√3
    D→a.→b=−72