ABCD is a trapezium such that AB, DC is parallel and BC is perpendicular to them. If angle (DAB) = 45∘ , BC = 2 cm and CD = 3 cm, then find the length of AB?
6 cm
4 cm
3 cm
5 cm
The correct Answer is:D
To find the length of AB in trapezium ABCD, where AB is parallel to CD, BC is perpendicular to both AB and CD, and angle DAB is 45 degrees, we can follow these steps:
1. Understand the Trapezium Configuration:
- Given trapezium ABCD, with AB || CD and BC ⊥ AB, CD.
- BC = 2 cm, CD = 3 cm, and angle DAB = 45°.
2. Draw the Trapezium:
- Draw a trapezium ABCD such that AB is at the top, CD is at the bottom, and BC is vertical.
- Label the points accordingly.
3. Identify the Right Triangle:
- In triangle DAB, we have:
- Angle DAB = 45°
- BC (height) = 2 cm
- CD (base) = 3 cm
4. Use Trigonometric Ratios:
- Since angle DAB is 45°, we can use the properties of a 45-45-90 triangle.
- In a 45-45-90 triangle, the lengths of the legs are equal, and the length of the hypotenuse is √2 times the length of each leg.
5. Calculate the Length of AB:
- Let AB = x.
- In triangle DAB:
- Using the sine function: sin(45°)=BCAD
- Here, AD=AB+CD=x+3
- Therefore, sin(45°)=2x+3
- Since sin(45°)=1√2, we can set up the equation:
1√2=2x+3
6. Cross-Multiply and Solve for x:
- Cross-multiplying gives:
x+3=2√2
- Rearranging gives:
x=2√2−3
7. Calculate the Numerical Value:
- Using √2≈1.414:
x≈2×1.414−3≈2.828−3≈−0.172
- Since length cannot be negative, we need to reevaluate our assumptions or calculations.
8. Reassess the Geometry:
- Since we have a trapezium, we should consider the trapezium's properties and the relationship between the sides.
- The correct approach is to use the Pythagorean theorem in triangle DAB:
AB=CD+BC⋅tan(45°)
- Since tan(45°)=1:
AB=3+2=5 cm
Final Answer:
The length of AB is 5 cm.
- Given trapezium ABCD, with AB || CD and BC ⊥ AB, CD.
- BC = 2 cm, CD = 3 cm, and angle DAB = 45°.
- Draw a trapezium ABCD such that AB is at the top, CD is at the bottom, and BC is vertical.
- Label the points accordingly.
- In triangle DAB, we have:
- Angle DAB = 45°
- BC (height) = 2 cm
- CD (base) = 3 cm
- Since angle DAB is 45°, we can use the properties of a 45-45-90 triangle.
- In a 45-45-90 triangle, the lengths of the legs are equal, and the length of the hypotenuse is √2 times the length of each leg.
- Let AB = x.
- In triangle DAB:
- Using the sine function: sin(45°)=BCAD
- Here, AD=AB+CD=x+3
- Therefore, sin(45°)=2x+3
- Since sin(45°)=1√2, we can set up the equation:
1√2=2x+3
- Cross-multiplying gives:
x+3=2√2
- Rearranging gives:
x=2√2−3
- Using √2≈1.414:
x≈2×1.414−3≈2.828−3≈−0.172
- Since length cannot be negative, we need to reevaluate our assumptions or calculations.
- Since we have a trapezium, we should consider the trapezium's properties and the relationship between the sides.
- The correct approach is to use the Pythagorean theorem in triangle DAB:
AB=CD+BC⋅tan(45°)
- Since tan(45°)=1:
AB=3+2=5 cm
The length of AB is 5 cm.
Topper's Solved these Questions
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises (EXPERT LEVEL)
45 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TEST YOURSELF
15 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises ( Foundation Level)
70 Videos
- LOGARITHMSBOOK - DISHA PUBLICATIONCHAPTER - LOGARITHMSEXERCISE - Test Yourself
15 Videos
- MOCK TEST - 3BOOK - DISHA PUBLICATIONCHAPTER - MOCK TEST - 3EXERCISE - Multiple Choice Questions
20 Videos
Similar Questions
ABCD is a trapezium such that ABandCD are parallel and BC⊥CD. If /_ADB= theta , BC =p and CD=q, then AB is equal to
View SolutionABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
View Solution
Knowledge Check
ABCD is a trapezium such that AB and DC are parallel and BC is perpendicular to them. If BC=1 cm, CD=2 cm and ∠ADB=45∘, then the lengths of AB is (in cm)
A125B85C53D163ABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ADB=θ,Bc=pandCD=q, then AB is equal to
A(p2+q2sinθpcosθ+qsinθB(p2+q2)cosθpcosθ+qsinthetCp2+q2p2cosθ+q2sinθD(p2+q2)sinθ(pcosθ+qsinθ)ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
Ap2+q2cosθpcosθ+qsinθBp2+q2p2cosθ+q2sinθC(p2+q2)cosθ(pcosθ+qsinθ)2D(p2+q2)sinθpcosθ+qsinθ
Quadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
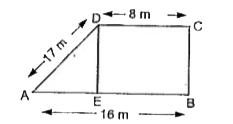
View SolutionIn the given figure ABCD is trapezium in which the parallel sides AB and CD both are perpendicular to BC. If AB = 16 m, CD = 8 m and AD = 17 M. What is the area of the trapezium ?
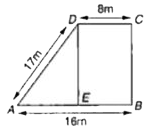
View SolutionIn the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ABD=θ,Bc=pandCD=q, then AB is equal to
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD. if ∠ADB=θ,BC=p and CD=q, then AB is equal to
View Solution
